传统的加热方法主要基于热辐射、对流和传导原理,被加热物按由外向内的方向传热。而微波加热技术通过电磁波与材料内部极性分子和带电粒子的直接相互作用来进行加热[1]。微波加热由于其独特的加热原理,具有高效加热、内部加热和环保加热的特点,因此被广泛应用[2]。然而,微波加热也有一些不可避免的缺点,加热不均匀和能量利用率低是最常见的两种[3]。加热不均匀通常容易引起局部过热和热点问题,并且随着加热时间的逐渐延长,容易引起热失控现象,导致最终产品质量下降甚至引起火灾和爆炸[4]。而加热效率低则会造成能量的浪费。在微波加热中,很难同时提高加热均匀性和效率,即高均匀性时加热效率较低,或加热效率较高时均匀性不好。为了改善微波加热过程中的加热均匀性和效率,人们提出了许多方法,最常见的是通过利用模式搅拌器或旋转转盘来提高加热的性能[5]。如今在众多微波源中,固态微波源凭借着频率及功率的可控性被广泛应用,且具有实时采集反馈的功能,为选频加热奠定了基础。本文针对微波加热的均匀性和效率的问题提出了一种双端口选频加热的方法。通过内置正交极化天线馈电的方式进行馈电,与传统的波导馈电相比,减少了馈电端口的体积。首先通过扫频的方式对各频点加热效率进行分析,寻找加热效率高的频点,同时与一致极化进行比较。对选择出的高效率频点进行分析,说明频率对负载的温度分布有影响。在选择出的高效率的频点上,进行频率选择性加热,即在同一个时间段内依次在高效率的频点上加热,从而在加热具有高效率的前提下来提高加热的均匀性,使加热不仅具有高效性,并且均匀性还有较大的提升。
1 模型和方法 1.1 几何建模图 1为用于多物理场计算的仿真模型,腔体大小为300 mm×250 mm×200 mm。腔体两端均有贴片天线,位于腔体两端的中心位置,天线的介质层为空气。两个贴片天线的尺寸均为50 mm×47 mm,馈电点偏离天线中心7.5 mm,两个天线的极化方式相互正交。在腔体内部放置一个40 mm×40 mm×20 mm的马铃薯,马铃薯在腔体中心且距离底部20 mm。两个端口馈电功率均为50 W,加热时间21 s。
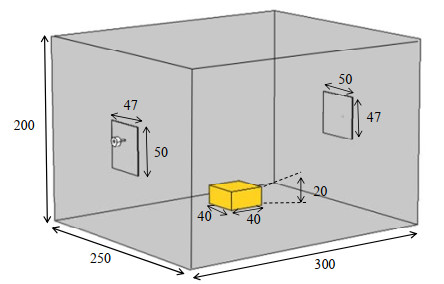 |
| Fig.1 Simulation model for multi-physical field calculation(unit: mm) 图 1 用于多物理场计算的仿真模型(单位:mm) |
该模型由电磁波传播和传热两部分耦合进行仿真。为了计算前一部分,采用麦克斯韦方程组:
| $\left\{ \begin{array}{l} \nabla \times \vec H = \vec J + \varepsilon \frac{{\partial \vec E}}{{\partial t}} \\ \nabla \times \vec E = - \frac{{\partial \vec B}}{{\partial t}} \\ \nabla \cdot \vec B = 0 \\ \nabla \cdot \vec D = {\rho _e} \\ \end{array} \right.$ | (1) |
式中:
电磁能量损耗由电磁损耗公式[6]来计算:
| ${Q_e} = \frac{1}{2}\omega {\varepsilon _0}\varepsilon ''{\left| {\vec E} \right|^2}$ | (2) |
式中:
负载温度分布由传热控制方程[7]计算:
| $\rho {C_p}\frac{{\partial T}}{{\partial t}} - k{\nabla ^2}T = Q = {Q_e}$ | (3) |
式中:
仿真模型中,加热腔体整个表面都被定义为理想电导体,即导体表面上切向电场为零,满足如下方程:
| $\vec n \times \vec E = \vec 0$ | (4) |
式中
对于传热边界条件,将对流传热边界条件应用于马铃薯片表面,近似马铃薯片对空气的自然对流热,满足如下方程[8]:
| ${k_n}\frac{{\partial T}}{{\partial \vec n}} + h \cdot (T - {T_{{\rm{air}}}}) = 0$ | (5) |
式中:
仿真的被加热物料为马铃薯,其电特性和物理特性所对应的参数如表 1所示。其中,使用复相对介电常数来更为实际地描述马铃薯在电磁波作用下的介电特性。复相对介电常数的实部表征了介质分子极化能力的大小,虚部表征的是能量在介质中的损耗情况。
| 表 1 马铃薯属性及对应参数 Table 1 Properties of the potato applied in the model |
本文腔体设计使用的是双端口馈电,馈电端口设计的是内置天线馈电。本节对两端口天线的极化方式,即正交极化方式和一致极化方式,进行分析。围绕2.4~2.5 GHz对系统进行设计,使其具有较高的加热效率。在2.4~2.45 GHz进行扫频分析,频率间隔为5 MHz,即在各自频点下分别加热21 s。
由图 2可知,对于正交极化和一致极化,均有各自的效率较高点。对于正交极化,加热高效率点为2.4~2.41 GHz以及2.45 GHz,加热效率均在65%以上,最高加热效率在2.41 GHz达到了85%,在其他频点处加热效率均低于35%。对于一致极化,加热效率最高频点在2.405 GHz,效率为71%,其余频点的加热效率均低于该频点的加热效率。两种极化方式的加热效率的趋势大致相同,而正交极化方式与一致极化方式相比,前者的最高加热效率比后者最高加热效率高出19.7%。因此,为实现加热高效率,本文选择正交极化方式馈电。
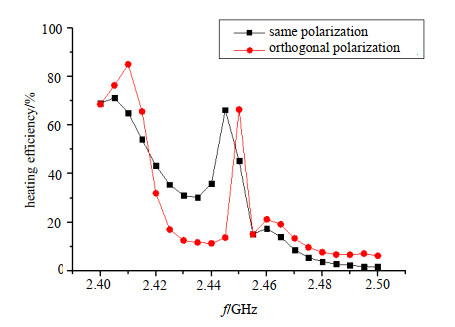 |
| Fig.2 Heating efficiency of the orthogonal polarization and the same polarization 图 2 正交极化与一致极化馈电的加热效率 |
由图 2可知,正交极化方式馈电下,在2.405 GHz, 2.41 GHz和2.45 GHz下有较高的加热效率,分别为76.35%, 85%和66.4%。利用COMSOL仿真软件,对该3个频点进行多物理场仿真,对相应频点下被加热负载的温度分布和加热均匀性进行对比,以下分别列出仿真计算结果。
图 3~图 4分别列出马铃薯在3个频点同一温度图例下各自的温度分布。由图 3~图 4可知,由于2.405 GHz与2.41 GHz频率相差不大,因此温度分布趋势大致相同,但是温升有差别。2.45 GHz的温度分布相比于前两个频点的温度分布差异较大,由此可以得出频率对微波加热有较大影响。为了定量讨论加热的均匀性,采用温度变异系数(Coefficient Of Variation,COV)来表征。COV是指负载中各点温度与平均温度的偏差,是由温度的平均上升量归一化得到的,公式(6)为COV的定义式。由其定义可知,COV越小则均匀性越高。
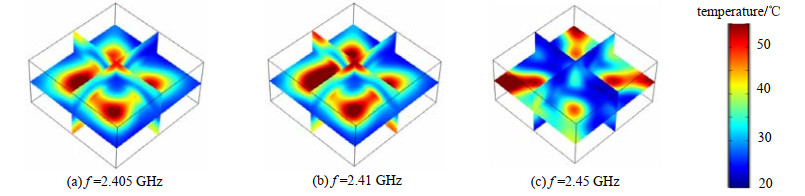 |
| Fig.3 3-D temperature distribution of the load 图 3 负载三维温度分布 |
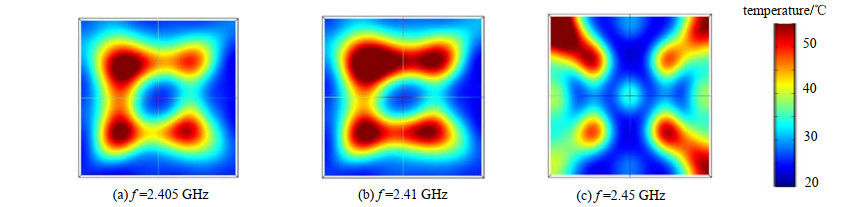 |
| Fig.4 Central surface temperature distribution of the load 图 4 负载中心面温度分布 |
| $COV = \sqrt {\frac{{\sum\nolimits_{i = 1}^n {{{({T_i} - \overline T )}^2}} }}{n}} /(\overline T - {T_0})$ | (6) |
式中:
| 表 2 各频点对应的仿真结果 Table 2 Simulation results of each frequency point |
由上一节可知,不同频率对加热的影响是不一样的。为了在维持高效率的前提下提高加热的均匀性,利用选频加热的方式,即在不同的时间段在不同的高效率频点处进行加热。提出在2.405 GHz, 2.41 GHz和2.45 GHz下分别加热7 s,一共加热21 s,仿真过程中采用温度继承的方式进行仿真,多物理场仿真结果如图 5所示。
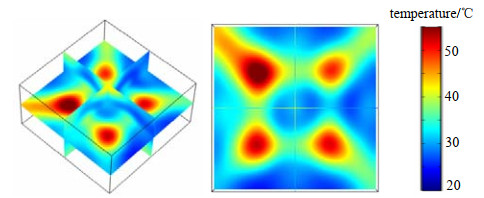 |
| Fig.5 Load temperature distribution of frequency-selected heating 图 5 选频加热负载温度分布 |
如图 5所示,负载中心截面的三维温度分布相比于3个频点独自加热更为均匀。计算其COV为0.35,加热效率为76%,第21 s的平均温度为33.04℃。COV相比于2.405 GHz下降了17.5%,相比于2.45 GHz下降了47.8%。由此可知,在维持具有固定频率加热的高效率前提下,选频加热的COV相比于固定频率加热有较大的降低,加热的均匀性有所提高。
3 结论本文设计了双端口内置正交极化天线馈电的腔体,与一致极化相比有更高的加热效率。通过频率选择分析,可知负载在不同频率下温度分布是不一样的。利用选频加热,即选择性地在高效率的频点上进行分时段加热,使负载在维持高效率的前提下均匀性有较大提升,证明了选频加热具有高效性和高均匀性。
| [1] |
郑亚琪, 陈星. 微波加热效应的多物理场仿真与实验[J]. 太赫兹科学与电子信息学报, 2018, 16(2): 302-306. (ZHENG Yaqi, CHEN Xing. Multi-physics simulation and experiment research of microwave heating[J]. Journal of Terahertz Science and Electronic Information Technology, 2018, 16(2): 302-306.) |
| [2] |
SALEMA A A, AFZAL M T. Numerical simulation of heating behavior in biomass bed and pellets under multimode microwave system[J]. International Journal of Thermal Sciences, 2015, 91: 12-24. DOI:10.1016/j.ijthermalsci.2015.01.003 |
| [3] |
VADIVAMBAL R, JAYAS D S. Non-uniform temperature distribution during microwave heating of food materials - a review[J]. Food and Bioprocess Technology, 2010, 3(2): 161-171. DOI:10.1007/s11947-008-0136-0 |
| [4] |
FARAG S, SOBHY A, AKYEL C, et al. Temperature profile prediction within selected materials heated by microwaves at 2.45 GHz[J]. Applied Thermal Engineering, 2012, 36: 360-369. DOI:10.1016/j.applthermaleng.2011.10.049 |
| [5] |
VÁCLAV S, ANDREA N, KVĚTOSLAV N. Finite element analysis of mode stirrer impact on electric field uniformity in a microwave applicator[J]. Drying Technology, 2012, 30(13): 1388-1396. DOI:10.1080/07373937.2012.664800 |
| [6] |
ZHU Huacheng, HE Jianbo, HONG Tao, et al. A rotary radiation structure for microwave heating uniformity improvement[J]. Applied Thermal Engineering, 2018, 141: 648-658. DOI:10.1016/j.applthermaleng.2018.05.122 |
| [7] |
PITCHAI K, BIRLA S L, SUBBIAH J, et al. Coupled electromagnetic and heat transfer model for microwave heating in domestic ovens[J]. Journal of Food Engineering, 2012, 112(1-2): 100-111. DOI:10.1016/j.jfoodeng.2012.03.013 |
| [8] |
TANG Zhengming, HONG Tao, LIAO Yinhong, et al. Frequency-selected method to improve microwave heating performance[J]. Applied Thermal Engineering, 2018, 131: 642-648. DOI:10.1016/j.applthermaleng.2017.12.008 |
 2020, Vol. 18
2020, Vol. 18


