2. 西华师范大学 计算机学院, 四川 南充 637009;
3. 电子科技大学 自动化工程学院, 四川 成都 611731
2. Computer School, China West Normal University, Nanchong Sichuan 637009, China;
3. School of Automation Engineering, University of Electronic Science and Technology of China, Chengdu Sichuan 611731, China
能量采集认知无线网络(EH-CRN)极具发展前景, 可在解决频谱资源短缺和能量效率(EE)问题的同时符合绿色通信的要求, 在国内外已有较为广泛的研究[1-6]。如果采用射频能量采集技术, 无线节点可采集周围环境射频源所发出的电磁波并转换为能量进行数据传输。由于发射机所辐射的射频信号具有持续可用性, 因此相比其他能量采集, 如热能和光能等, 射频能量采集更具灵活性和持续性[7-8]。在周围射频认知无线网络中, 次用户(SU)可采用3种运行模式:交织(Interweave)、覆盖(Overlay)和重叠(Underlay)[8], 本文讨论在Underlay模式下, 只要主用户(PU)接收机所受干扰处于可接受范围内, 次用户可同主用户进行数据的并发传输。
射频能量源主要分为专用射频和环境射频。由于是按需供应和定向传输, 专用射频可为节点提供能量直至达到预测能量值, 如有线供电通信网络(Wire Powered Communication Network, WPCN)[9-14]和无线信息与能量的同时传输网络(Simultaneous Power Transfer Networks, SWIPT)(信息和能量均属于射频信号[15-17])。然而, 上述WPCNs或SWIPTs的工作均基于系统可在给定频段内进行专用假设, 无需考虑与其他系统在同频段下的相互干扰。
环境射频信号包括附近如基站、主授权网络和其他射频源等环境射频源所辐射信号。主网络辐射的射频信号可作为认知用户进行能量采集的绿色能量源, 主要为低能耗网络(如传感器网络)提供能量。目前研究主要集中在射频能量采集认知无线网络(RF EH-CRNs)中, SUs首先从PUs的信号中获取能量, 然后与PUs共用频谱进行传输。文献[18]重点研究了收集-感知-吞吐量的权衡以及感知时间、感知阈值以及融合规则的联合优化, 在保证PU服务得到充分保障下, 最大化SU预期可达吞吐量。文献[19]中, PU不仅能够在信道空闲时在授权给主要用户的信道上传输数据包, 还能够在信道繁忙时从主要用户传输中获取射频能量。文献[20]提出一种基于能量采集的两跳认知中继网络。文献[21]分析了一种具有射频能量采集功能的多跳认知无线电网络, 该网络中所有SU都是由所接收PU信号的能量进行自供电。上述关于RF EH-CRN的工作主要集中在可达吞吐量和能量收集之间的性能权衡上。同时, 传输数据量越大, 能耗越大。为降低硬件设计复杂性, 节点能量收集效率通常较低。在环境中采用RF EH-CRNs以节能方式实现数据传输非常重要, 可避免过度能源消耗和系统中断[2]。
能量效率定义为平均传输的数据量与平均能耗之间的比值, 是节能传输无线通信的重要指标, 但目前针对QoS等复杂约束下的Underlay RF EH-CRN相关研究较少[22]。本文目标是在能量因果约束、干扰约束下和保证SU的服务质量前提下, 最大限度提高射频认知无线网络能量效率。
1 系统模型如图 1所示, 考虑带有一个主用户发射机(PT)-接收机(PR)传输对和一个次用户发射机(ST)-接收机(SR)对的时隙RF EH-CRN。在RF EH-CRN中有以下几种链路:a) PT和ST之间的链路称为能量收集链路; b) PT(ST)和SR(PR)之间的链路称为干涉链路; c) PT(PR)和ST(SR)之间的链路称为数据传输链路。PT总处于活动状态, 可在授权频谱中为PR服务, 并在给定的干扰功率约束下与SU共享频谱资源。假设所有信道遵循块衰落, 即在每个时隙各分块的信道衰落状态维持不变, 但分块之间会发生变化。
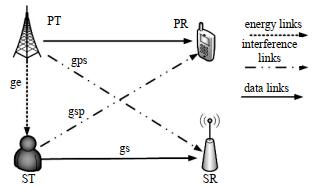 |
| Fig.1 System model 图 1 系统模型 |
假设CRN系统中, SR拥有一个固定电源供电(根据应用场景的不同, 也可给SR端配置能量收集功能, 系统模型会进行相应修改), ST从PT的RF信号中收集能量进行自供电。为降低硬件设计和系统复杂性, 让ST在一个时刻只能进行能量采集或数据传输, 即ST以先采集后传输的方式工作。系统考虑一个持续时间为T的帧, 该帧被分割为两部分并分配给ST, 分别进行能量采集和数据传输, 如图 1和图 2所示。
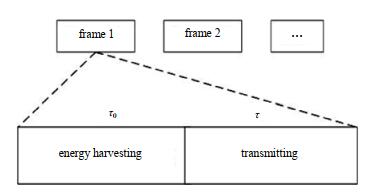 |
| Fig.2 Time slot structure of RF EH-CRN 图 2 系统时隙结构 |
假设PT持续保持通信工作状态。目前已有的干扰消除技术已能将干扰信号强度削减至底噪级别, 假设PT端的数据传输不会对SR的数据接收造成干扰。类似文献[21], 将ST收集到的能量保存在一个超级电容中, 这种超级电容具有可满足小型化要求、且理论上可以无限次充放电周期等优点。经过了持续时间为τ0的能量采集, ST能收集到的能量可根据式(1)进行计算:
| $ {E_H} = \eta {g_e}{P_T}{\tau _0} $ | (1) |
式中:η为能量收集效率; ge为能量收集增益; PT为PT传输功率。
1.2 数据传输阶段在数据传输阶段, ST消耗收集到的能量进行数据传输。由于超级电容的泄漏以及储能或管理方法的缺乏, 假设该系统在进行一帧数据传输后, 剩余的能量可能无法在下一帧数据传输阶段使用。显然, ST的总消耗能量必须等于或小于EH, 即能量因果关系约束为:
| $ \left( {P{g_s} + {P_c}} \right)\tau \le {E_{^H}} $ | (2) |
式中:P为ST传输功率; Pc为ST发射电路能量损耗; gs为次用户数据传输链路增益。
ST与PU在CRN的Underlay工作模式下共享频谱, 为保护主用户不受干扰, 必须对ST的发射功率进行限制, 以进行干涉碰撞约束。
| $ P{g_{sp}} \le {P_I} $ | (3) |
式中:PI为PR所允许的干扰峰值门限; gsp为次用户干扰信道增益。计算SU在一帧中可实现的吞吐量:
| $ R\left( {\tau , P} \right) = \tau {\log _2}\left( {1 + \frac{{P{g_s}}}{{{P_T}{g_{ps}} + {\sigma ^2}}}} \right) $ | (4) |
式中:gps为主用户干扰信道增益; σ2为SR处的噪声功率。
无线网络中, 节点以高效能的方式传输数据时, 为节省能量, 总是以尽可能小的吞吐量传输数据。然而, 在许多场景中, 如无线传感器网络执行数据收集、事件监视和其他应用程序, 为满足传输QoS而对无线节点提出最小吞吐量要求是必不可少的。为满足SU的QoS, 为SU设置一个最小所需速率, 即吞吐量约束。
| $ R\left( {\tau , P} \right) \ge {R_{out}} $ | (5) |
网络能量效率被定义为传输的比特数与消耗能量的比值。在一个时隙中, RF EH-CRNs的总能耗EC由两部分组成:a)能量采集阶段中, 能量采集电路所消耗的能量PH; b)传输阶段所消耗能量。EC表达式如下:
| $ {E_C} = {P_H}{\tau _0} + \left( {P{g_s} + {P_c}} \right)\tau $ | (6) |
将式(2)~式(6)进行整合, 可以构建RF EH-CRNs的能量效率问题:
| $ \left\{ \begin{array}{l} OP1:\mathop {\max }\limits_{{\tau _0}, \tau , P} EE\left( {{\tau _0}, \tau , P} \right) = \frac{{\tau {{\log }_2}\left( {1 + {\textstyle{{P{g_s}} \over {{P_T}{g_{ps}} + {\sigma ^2}}}}} \right)}}{{{P_H}{\tau _0} + \left( {P{g_s} + {P_c}} \right)\tau }}\\ s.t.\left\{ \begin{array}{l} C1:\left( {P{g_s} + {P_C}} \right)\tau \le \eta {g_e}{P_T}{\tau _0};\;\quad C2:P{g_{sp}} \le {P_I}\\ C3:R\left( {\tau , P} \right) \ge {R_{out}};\quad \quad C4:0 \le \tau \le T;\quad \quad C5:0 \le P \le {P_{\max }} \end{array} \right. \end{array} \right. $ | (7) |
式中:C1表示在当前分配的时间和传输功率下, 数据传输能耗不能高于系统所收集的能量; C2表示ST的传输功率不能超过PR可承受的干扰功率门限, 本系统通过该机制保护PR免于干扰影响; C3表示本系统的吞吐量约束, 为系统的QoS保证; C4表示被ST消耗的总时间不能多于一个帧周期; C5表示ST的最大功率约束。
2 问题求解优化问题OP1是一个非线性分式规划问题, 很明显这个问题关于变量是非凸的, 一般为NP-Hard问题。在解决优化问题OP1之前, 对以下引理进行证明。
引理 1: 优化问题OP1的最大能量效率总是在τ0+τ=T处取得。
证明: 可将EE问题转化为下述形式:
| $ EE({\tau _0}, \tau , P) = \frac{{{{\log }_2}\left( {1 + {\textstyle{{P{g_s}} \over {{P_T}{g_{ps}} + {\sigma ^2}}}}} \right)}}{{({P_T} - \eta {g_e}{P_T}){\textstyle{{{\tau _0}} \over \tau }} + (P{g_s} + {P_c})}} $ | (8) |
假设当τ0+τ < T时, 可得到问题OP1的最大值EE(τ0, τ, P。由于能量守恒定律, 实际情况下增量
| $ \left\{ \begin{array}{l} OP2:\mathop {\max }\limits_{\tau , P} EE\left( {\tau , P} \right) = \frac{{\tau {{\log }_2}\left( {1 + {\textstyle{{P{g_s}} \over {{P_T}{g_{ps}} + {\sigma ^2}}}}} \right)}}{{{P_H}\left( {T - \tau } \right) + \left( {P{g_s} + {P_c}} \right)\tau }}\\ s.t.\left\{ \begin{array}{l} C1:\left( {P{g_s} + {P_c}} \right)\tau \le \eta {g_e}{P_T}\left( {T - \tau } \right);\quad C2:P{g_{sp}} \le {P_I}\\ C3:R\left( {\tau , P} \right) \ge {R_{out}};\quad \quad C4:0 \le \tau \le T;\quad \quad C5:0 \le P \le {P_{\max }} \end{array} \right. \end{array} \right. $ | (9) |
式中约束条件C2, C3, C4, C5分别与问题OP1中的约束条件C2, C3, C4, C5等价。对于非线性分数规划问题, 用低复杂度算法求解OP2问题的封闭形式解是困难的。本文采用坐标上升法求解OP2。具体来说, OP2可被分解为2个子问题, 即:给定时间τ下的功率分配子问题OP3, 与给定发射功率P分配策略下的传输时间选择问题OP4。
| $ \left\{ \begin{array}{l} OP3:\mathop {\max }\limits_P E{E_3}\left( P \right) = \frac{{\tau '{{\log }_2}\left( {1 + {\textstyle{{P{g_s}} \over {{P_T}{g_{ps}} + {\sigma ^2}}}}} \right)}}{{{P_H}\left( {T - \tau '} \right) + \left( {P{g_s} + {P_c}} \right)\tau '}}\\ s.t.\left\{ \begin{array}{l} C1:\left( {P{g_s} + {P_c}} \right)\tau ' \le \eta {g_e}{P_T}\left( {T - \tau '} \right);\quad C2:P{g_{sp}} \le {P_I}\\ C3:R\left( P \right) \ge {R_{out}};\quad \quad C4:0 \le P \le {P_{\max }} \end{array} \right. \end{array} \right. $ | (10) |
式中:τ'为给定的时间分配约束; C1和C3分别为功率分配需要满足的能量约束条件和吞吐量约束条件; C2和C4分别与OP2中的C2和C5约束条件相同。
| $ \left\{ \begin{array}{l} OP4:\mathop {\max }\limits_\tau E{E_{\rm{4}}}\left( \tau \right) = \frac{{\tau {{\log }_2}\left( {1 + {\textstyle{{P'{g_s}} \over {{P_T}{g_{ps}} + {\sigma ^2}}}}} \right)}}{{{P_H}\left( {T - \tau } \right) + \left( {P'{g_s} + {P_c}} \right)\tau }}\\ s.t.\left\{ \begin{array}{l} C1:\left( {P'{g_s} + {P_c}} \right)\tau \le \eta {g_e}{P_T}\left( {T - \tau } \right)\\ C2:R\left( \tau \right) \ge {R_{out}}_I;\quad C3:0 \le \tau \le T \end{array} \right. \end{array} \right. $ | (11) |
式中:P' 为给定功率分配策略; C1和C2为传输时间分配需要满足的能量和吞吐量约束条件; C3约束与OP2中的C3相同。
引理2: 基于Charnes-Cooper变换(Charnes-Cooper Transformation, CCT), 使P=y/v, v=1/Ec(p), OP3可变形为:
| $ \left\{ \begin{array}{l} OP5:\mathop {\max }\limits_{{\textstyle{y \over v}} \in {R^ + },v > 0} E{E_{\rm{5}}}\left( \tau \right) = v\tau '{\log _2}\left[ {1 + {\textstyle{{y{g_s}} \over {v\left( {{P_T}{g_{ps}} + {\sigma ^2}} \right)}}}} \right]\\ s.t.\left\{ \begin{array}{l} C1:v{E_C}\left( {{\textstyle{y \over v}}} \right) = 1;\quad C2:\left( {\frac{y}{v}{g_s} + {P_C}} \right)\tau ' \le \eta {g_e}{P_T}\left( {T - \tau '} \right)\\ C3:\frac{y}{v}{g_{sp}} \le {P_I};\quad C4:R\left( {\frac{y}{v}} \right) \ge {R_{out}}_I;\quad C5:0 \le \frac{y}{v} \le {P_{\max }} \end{array} \right. \end{array} \right. $ | (12) |
式中:C1为具有相互关系的y*和v*两个解, C2~C4为OP3中C2~C4相应的转换形式。若(y*,v*)为OP5的一个最优解, 则y*/v*为OP3的最优解。由于OP3中的R(P)是凹的, OP5是能被凸优化技术求解的等效凹规划问题。
证明 :引理2的证明必须引入分式规划的概念。首先, 当某优化问题的目标函数可被表示为2个函数比值时, 该优化问题被称为分式规划(Fractional Program, FP)。一个FP问题可被描述为:
| $ \left\{ \begin{align} & \underset{x\in X}{\mathop{\max }}\, {f(x)}/{g(x)}\; \\ & s.t.\ \ \ {{h}_{i}}(x)\le 0, \forall i=1, 2, \cdots , N \\ \end{align} \right. $ | (13) |
式中:f(x), g(x)和hi(x)均为实值函数; X∈RN。
式(13)所表示的FP问题若满足以下条件, 则可称为凹分式规划问题(Concave Fractional Program, CFP):
1) f(x)是凹函数, 且g(x)在X上是凸函数;
2) 若g(x)为非仿射函数, f(x)在S上函数值为正, 其中
一个具有仿射函数作为分母的CFP可通过使用CCT方法转换目标函数为凹函数的优化问题[23]。因此, 使用CCT方法, 可得到式(13)等效的凹规划问题:
| $ \left\{ \begin{array}{l} \mathop {\max }\limits_{{\textstyle{y \over t}} \in X,t > 0} tf\left( {{\textstyle{y \over t}}} \right)\\ s.t.\;\;\;\left\{ \begin{array}{l} t{h_i}\left( {{\textstyle{y \over t}}} \right) \le 0,\forall i = 1,2, \cdots ,N\\ tan{\textstyle{y \over t}} = 1 \end{array} \right. \end{array} \right. $ | (14) |
若式(13)所描述问题具有最优解, 当且仅当式(14)具有最优解。2个解通过关系式y=tx和t=1/g(x)联系在一起。对OP3来说, 因为log对数函数是凹函数, 则R(P)关于P是凹的[24]。此外, EC(P)在P上是仿射函数。与式(14)相同, 基于CCT方法, 使P=y/v及v=1/Ec(P), 可将优化问题OP3等效变换为凹规划问题OP5。因此引理2得证。
等效优化问题OP5描述的系统总能量效率最大化的最优功率:
| $ {{P}^{*}}=\left( \frac{y*}{v*} \right)=\min \left( \psi , \frac{{{P}_{I}}}{{{g}_{sp}}}, {{P}_{\max }} \right) $ | (15) |
式中:
对于最优传输时间分配, 优化问题OP4系统总能量效率最大化的最优时间分配可求解如下:
| $ {{\tau }^{*}}\text{=}\frac{\eta {{g}_{e}}{{P}_{T}}T}{P'{{g}_{s}}+{{P}_{c}}+\eta {{g}_{e}}{{P}_{T}}T} $ | (16) |
综上所述, 算法对求解方法进行了总结, 步骤如下:a)初始化参数。以下步骤循环:b)基于CCT方法针对给定P*解决凹问题OP3;c)针对式(12)寻找最优解P*; d)针对给定P求解模型OP4;e)根据式(13)寻找最优解τ*; f)
在算法中, 基于给定[τ, P]分量, ST迭代地寻找最优策略。特别的, 在给定τ值时找到最优值P*, 然后基于给定P值得到最优值τ*。同时, Δτ, ΔP应该足够小。如果满足
进行仿真验证所提方法的有效性和性能。网络参数设置如下:能量收集效率η=0.7, 时隙长度T=1, 能量收集增益ge=0.9, 主用户干扰信道增益gps=0.3, 次用户干扰信道增益gsp=0.2, 次用户数据传输链路增益gs=0.9, 噪声功率σ2=-65 dBm, 电路损耗Pc=0.02 W, ST的最大传输功率Pmax=6 W。
RF EH-CRN系统中EE和吞吐量关于τ和P典型变化如图 3~图 4所示, 其中PT和PI分别设置为10 W和2 W。从图 3和图 4中可看出, 当τ=0.97, P=0.2 W时, EE达到最大值0.25, 而当τ=0.53, P=Pmax=6 W时, 吞吐量达到最大值0.75。最佳EE解决方案并不意味着同时也是最佳吞吐量解决方案。因为EE是关于传输时间和功率的非增函数, 吞吐量是关于传输时间和功率的非减函数。
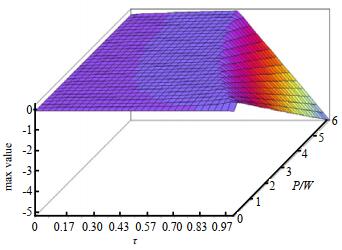 |
| Fig.3 The EE of RF-CRNs with respect to τ and P 图 3 RF EH-CRNs关于τ和P的能量效率 |
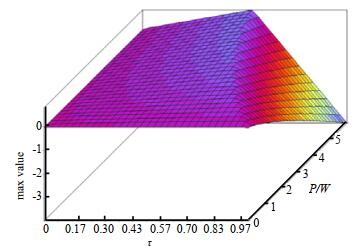 |
| Fig.4 Throughput of RF-CRNs with respect to τ and P 图 4 RF EH-CRNs关于τ和P的吞吐量 |
图 5为在给定每个SU的最小吞吐量门限Rout下, 不同PT和PI值下RF-CRNs的EE。从图 5可以看出, 相同PT、不同PI下, 可达到的最大EE值是相同的。在能源效率优化过程中, ST总是以相同的最小吞吐量(Rout=0.4)传输数据, 以节约能源。PT相同, 能耗相同, 因此最优能源效率相同。从图 5中还可以明显看出, 随着PT的增加, EE呈下降趋势。因为PT越大, 对SR的干扰就越大, 进而导致吞吐量下降。为满足最小数据速率约束Rout, 增加发射时间τ和提高发射功率P, 但将导致更多能耗。同时, PT越大, 在能量收集阶段能量损失越多, 最终将导致能量效率性能下降。当干扰足够大且PI较高时, 次用户不能满足OP2中C1~C5任何一个约束条件, EE急剧下降到接近于零, 将导致系统中断。
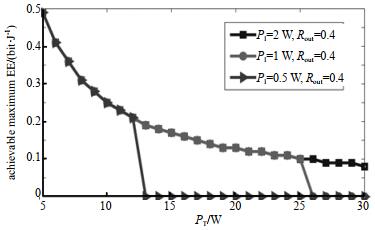 |
| Fig.5 Achievable EE analysis versus PT 图 5 可实现能量效率和PT对比分析图 |
图 6为最小速率需求Rout下, PU接收机在不同峰值允许干扰阈值下可达到的最大EE。当峰值允许干扰阈值PI非常小时, SU的发射功率必须足够小, 这违反吞吐量约束, 导致系统中断。在PT相同的情况下, 随着PI的增大, 可达到的最大能效保持不变。通过SU的传输功率P可以随PI的增加而增加, 传输功率越大, 吞吐量越大, 需要能量越多, 不利于EE优化。因此, 在能效优化过程中, SU的传输功率不会随PI的增大而增大, 吞吐量和能耗也会保持不变。
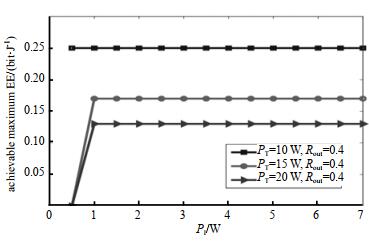 |
| Fig.6 Achievable EE analysis versus PI 图 6 可实现能量效率和PI结果对比分析 |
为进一步证明能效优化和吞吐量优化之间的区别, 图 7和图 8为不同PT和PI下的吞吐量优化。从图 7可以看出, 吞吐量随PI的增加而增加, 这是由于增加的PI扩大了次用户发射机ST传输功率P的可行域, 并可进一步提高R(τ, P)。与能量效率EE一样, R(τ, P)也会随PT的增加而减少。PT越大, 则SU收集的能量越多, 对SR的干扰也越大。因此, 当干扰足够大或PI为紧致集时, SU不能满足规定的最小吞吐量阈值, 吞吐量急剧下降到接近于零, 系统中断。
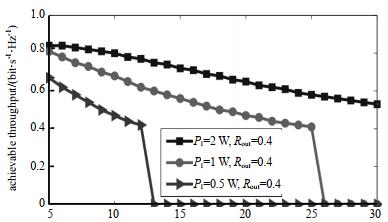 |
| Fig.7 Throughput optimization versus PT. 图 7 PT变化与吞吐量优化图 |
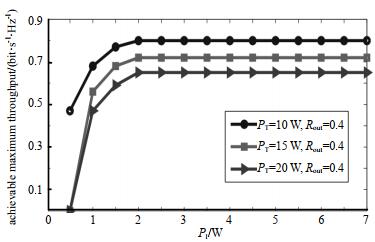 |
| Fig.8 Throughput optimization versus PI 图 8 PI变化与吞吐量优化 |
图 8为PI与吞吐量之间的关系, 随着P和PI的增大, R(τ, P)和能量消耗对应增加, 但R(τ, P)不能进一步提高。由于收获能量有限和最大传输功率的约束, P不可能是无限的。
4 结论本文研究了Underlay模式下RF EH-CRNs的EE最大化问题。通过对可达吞吐量和能量损耗的分析, 将该问题表示为凹/仿射分式规划问题, 利用坐标上升和CCT法将其转化为等效凹问题。在保证系统通信服务质量的前提下, 通过限制最小速率, 获得最优EE。另外, 分析了最小速率传输需求对输出功率的影响。仿真结果验证了相关算法的有效性。未来的工作将考虑多SU场景和储能管理, 进一步提高EE。此外, 应对先进的能量管理方法进行研究来处理基于PU动态模型下的能量收集问题, 以满足RF EH-CRN在不同模式下高效工作的需求。
| [1] |
PARK S, HONG D. Achievable throughput of energy harvesting cognitive radio networks[J]. IEEE Transactions on Wireless Communications, 2014, 13(2): 1010-1022. DOI:10.1109/TWC.2013.121713.130820 |
| [2] |
MOHJAZI L, DIANATI M, KARAGIANNIDIS G K, et al. RF-powered cognitive radio networks:technical challenges and limitations[J]. IEEE Communications Magazine, 2015, 53(4): 94-100. DOI:10.1109/MCOM.2015.7081081 |
| [3] |
LU X, WANG P, NIYATO D, et al. Wireless networks with RF energy harvesting:a contemporary survey[J]. IEEE Communications Surveys & Tutorials, 2014, 17(2): 757-789. |
| [4] |
庄陵, 马龙. 考虑频谱感知错误的多载波认知无线电资源分配算法[J]. 计算机工程, 2017, 43(2): 171-175. (ZHUANG Ling, MA Long. Resource allocation algorithm of multicarrier cognitive radio considering spectrum sensing error[J]. Computer Engineering, 2017, 43(2): 171-175. DOI:10.3969/j.issn.1000-3428.2017.02.028) |
| [5] |
冯刚, 覃锡忠, 贾振红, 等. 认知无线电环境下无线能量通信网的能效研究[J]. 计算机工程, 2019, 45(3): 142-147. (FENG Gang, QIN Xizhong, JIA Zhenhong, et al. Research on energy efficiency of wireless powered communication network in cognitive radio environment[J]. Computer Engineering, 2019, 45(3): 142-147.) |
| [6] |
谢振威, 朱琦. 基于能量协作的认知能量采集网络功率分配算法[J]. 通信学报, 2017, 38(9): 176-184. (XIE Zhenwei, ZHU Qi. Power allocation algorithm for cognitive radio energy harvesting networks based on energy cooperation[J]. Journal on Communications, 2017, 38(9): 176-184.) |
| [7] |
FENG D, JIANG C, LIM G, et al. A survey of energy-efficient wireless communications[J]. IEEE Communications Surveys & Tutorials, 2013, 15(1): 167-178. |
| [8] |
THAI H D, NIYATO D, WANG P, et al. Opportunistic channel access and RF energy harvesting in cognitive radio networks[J]. IEEE Journal on Selected Areas in Communications, 2014, 32(11): 2039-2052. DOI:10.1109/JSAC.2014.141108 |
| [9] |
JU H, ZHANG R. Throughput maximization in wireless powered communication networks[J]. IEEE Transactions on Wireless Communications, 2014, 13(1): 418-428. DOI:10.1109/TWC.2013.112513.130760 |
| [10] |
CHEN H, LI Y, REBELATTO J L, et al. Harvest-then-cooperate:wireless-powered cooperative communications[J]. IEEE Transactions on Signal Processing, 2015, 63(7): 1700-1711. DOI:10.1109/TSP.2015.2396009 |
| [11] |
YAO Q, HUANG A, SHAN H, et al. Delay-aware wireless powered communication networks-energy balancing and optimization[J]. IEEE Transactions on Wireless Communications, 2016, 15(8): 5272-5286. DOI:10.1109/TWC.2016.2555803 |
| [12] |
WU Q, TAO M, NG D W K, et al. Energy-efficient resource allocation for wireless powered communication networks[J]. IEEE Transactions on Wireless Communications, 2016, 15(3): 2312-2327. DOI:10.1109/TWC.2015.2502590 |
| [13] |
LIN X, HUANG L, GUO C, et al. Energy-efficient resource allocation in tdms based wireless powered communication networks[J]. IEEE Communications Letters, 2017, 21(4): 861-864. |
| [14] |
MIN S, MENG Z. Energy efficiency optimization for wireless powered sensor networks with non-orthogonal multiple access[J]. IEEE Sensors Letters, 2018, 2(1): 1-4. |
| [15] |
XU J, LIU L, ZHANG R. Multiuser miso beamforming for simultaneous wireless information and power transfer[J]. IEEE Transactions on Signal Processing, 2014, 62(18): 4798-4810. DOI:10.1109/TSP.2014.2340817 |
| [16] |
LEE S, LIU L, ZHANG R. Collaborative wireless energy and information transfer in interference channel[J]. IEEE Transactions on Wireless Communications, 2015, 14(1): 545-557. DOI:10.1109/TWC.2014.2354335 |
| [17] |
DING Z, KRIKIDIS I, SHARIF B, et al. Wireless information and power transfer in cooperative networks with spatially random relays[J]. IEEE Transactions on Wireless Communications, 2014, 13(8): 4440-4453. DOI:10.1109/TWC.2014.2314114 |
| [18] |
YIN S, QU Z, LI S. Achievable throughput optimization in energy harvesting cognitive radio systems[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(3): 407-422. DOI:10.1109/JSAC.2015.2391712 |
| [19] |
HOANG D T, NIYATO D, WANG P, et al. Performance optimization for cooperative multiuser cognitive radio networks with RF energy harvesting capability[J]. IEEE Transactions on Wireless Communications, 2015, 14(7): 3614-3629. DOI:10.1109/TWC.2015.2408610 |
| [20] |
JANGHEL K, PRAKRIYA S. Throughput of underlay cognitive energy harvesting relay networks with an improved time- switching protocol[J]. IEEE Transactions on Cognitive Communications & Networking, 2017, 4(1): 66-81. |
| [21] |
XU C, ZHENG M, LIANG W, et al. End-to-end throughput maximization for underlay multi-hop cognitive radio networks with RF energy harvesting[J]. IEEE Transactions on Wireless Communications, 2017, 16(6): 3561-3572. DOI:10.1109/TWC.2017.2684125 |
| [22] |
ZHOU F, BEAULIEU N C, LI Z, et al. Energy-efficient optimal power allocation for fading cognitive radio channels:ergodic capacity, outage capacity, and minimum-rate capacity[J]. IEEE Transactions on Wireless Communications, 2016, 15(4): 2741-2755. DOI:10.1109/TWC.2015.2509069 |
| [23] |
BOYD S, VANDENBERGHE L, FAYBUSOVICH L. Convex optimization[J]. IEEE Transactions on Automatic Control, 2006, 51(11): 1859. DOI:10.1109/TAC.2006.884922 |
| [24] |
SCHAIBLE S, SHI J. Recent developments in fractional programming: single-ratio and max-min case[C]// Proceedings of the 3rd international conference on Nonliner Analysis and Convex Analysis. Tokyo, Japan: [s.n.], 2003: 493-506.
|
 2020, Vol. 18
2020, Vol. 18

