微机电系统(MEMS)封装残余应力是在封装工艺过程中芯片上产生的残余应力,主要来源于硅和封装材料之间的热膨胀不匹配现象[1]。残余应力的产生不仅会使结构产生预期之外的形变,同时还会造成MEMS器件的热漂移,这对于MEMS器件的热稳定性和长期贮存稳定性有着十分重大的影响[2−6]。此外,MEMS封装应力的改变会导致微结构的形变产生相应变化,甚至会伴随材料老化产生器件分层、断裂等失效模式,这个现象则会对高精确度的MEMS器件的性能产生不利影响[7]。对MEMS封装残余应力进行高精确度的测量,可以定量地监测应力在工艺加工和服役环境中的产生、演变规律,并对优化改进方案给出准确评价,有利于封装应力的研究。目前存在的高精确度应力测量方法主要包括差分电容测量法[4]、基底曲率法[8-10]、X射线衍射法(XRD)[10-12]、拉曼光谱法[13-19]、在片测量结构法[20-24]等。差分电容测量应力的方法会在封装过程中由于电学因素的影响而产生精度问题,而基底曲率法一般用于测量衬底上薄膜的应力。XRD和拉曼光谱法测量应力具有很高的精确度且能够测量局部应力情况,它们都是非接触性检测的方法,不会对测试样品造成损伤,是目前MEMS残余应力高精确度测量中最常用的方法。高精确度的XRD和拉曼光谱法的最小应力分辨力约在5~10 MPa。然而,高性能MEMS器件为了追求较好的稳定性,其封装残余应力通常很小。例如,利用有限元分析(FEM)对一款高精确度MEMS加速度计的封装模型进行应力仿真,得出芯片上的封装残余应力平均应力值只有0.31 MPa左右,因此它们均不适用于对低封装残余应力的直接测量。
在片测量结构法一般是将MEMS的微小形变进行尺度放大,再通过MEMS显微技术观测形变,并计算残余应力大小,其中关键在于放大结构的设计。目前已经有相关研究进行了应力放大结构的设计,例如旋转指针结构[20-21]、双指针结构[22]、折叠结构[23]和杠杆指针测量结构[23-24]等,通过设计细长指针来观测被放大的微结构形变。然而,对于本文所研究的封装应力而言,受限于工艺和显微技术的精确度(约0.15μm[20]),其应力测量精确度不足以测量0.31 MPa的封装应力。此外,目前研究中的放大结构基本都是只针对形变进行放大,其应力未得到显著放大,无法结合拉曼光谱技术进行放大后应力的测量。
针对低封装残余应力的测量问题,在现有应力测试技术的基础上,本文提出了一种融合显微拉曼光谱和在片应力放大结构的方法,即首先利用在片放大结构对封装应力进行定量的放大,再利用显微拉曼光谱对应力集中区的应力进行无损测量,从而可以推算出封装应力的大小。本文提出的封装应力测量方法能够测量到MEMS器件中产生的封装应力的平均水平,可用于对封装工艺残余应力的评估或是封装残余应力的长期监测等科学研究。后文针对低封装残余应力测量的特点,提出了应力放大结构的设计方法并推导其应力放大关系。针对一款高精确度微加速度计的封装应力测量,本文先后通过仿真和实验对该测量方法进行了验证,并成功测量到微加速度计的平均封装应力大小。
1 测量方法理论分析本文提出的测量方法核心在于应力放大结构的设计和应力放大关系的推导。
1.1 应力放大结构设计图 1(a)为残余应力待测量的原始封装模型,是由硅芯片、封装胶和陶瓷基底组成的胶接结构,Ao表示芯片长度方向的横截面积,L表示芯片的长度。图 1(b)所示为应力放大结构的设计图,其中芯片结构分为两大部分,分别是外框(frame)和敏感结构,敏感结构包括指针(probe)和其支撑梁(bearing beam)。为了能够实现封装应力的放大,并且应力的放大倍率在一定的待测应力范围内较为稳定,本文对应力放大结构的设计提出了3项前提条件:1)原始封装模型和应力放大模型中的芯片外围尺寸(总长、总宽和厚度)相同,使得两种模型中的芯片所受到来自封装胶的力基本一致;2)外框的刚度远大于敏感结构刚度,使得外框基本上分担全部的封装应力并产生形变;3)敏感结构中,支撑梁的刚度远大于指针的刚度,使得支撑梁能够将外框形变转化为位移并传递给指针,使指针能完全根据外框的形变产生变形,实现应力集中。
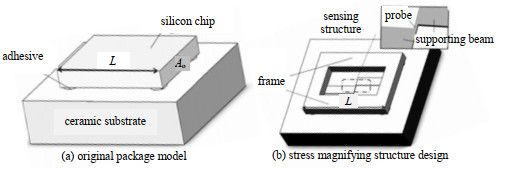 |
| Fig.1 Original package model and stress magnifying structure design 图 1 原始封装模型和应力放大结构设计 |
该结构实现应力放大的基本原理为,应力放大结构的芯片和原始封装模型的芯片在相同的封装工艺下,所受到的来自封装胶的力基本等效,在应力放大结构中由于芯片承载力的截面减小而实现了封装应力的第一级放大。相应产生的外框形变通过敏感结构的支撑梁传递到指针,利用指针尺寸小、易变形的特性实现了应力的第二级放大。
1.2 应力放大关系图 1展示了原始封装模型和应力放大设计封装模型的对比,两者区别在于芯片的内部结构不同。两个模型的芯片外围尺寸完全相同,因此在相同的封装条件下(封装温度、封装胶、基底、布胶方式),由于热膨胀变形只与温度和总体尺寸有关,因此芯片整体的热形变、所受到来自封装胶的力对于原始封装模型和应力放大封装模型而言是相同的。
依据前提条件1),可建立原始封装模型和应力放大模型中的应力联系如下:
| ${\sigma _{\rm{o}}}{A_{\rm{o}}} = {\rm{Thermal\;Force}} = {\sigma _{\rm{f}}}{A_{\rm{f}}}$ | (1) |
式中:σo和Ao分别表示原始封装模型中的芯片中平均封装应力和横截面积;σf和Af分别表示放大设计模型中芯片外框中的封装应力和横截面积。
前提条件2)的目的在于使指针上的集中应力能够正确反映外框上封装应力的放大,减小支撑梁和指针所分担的来自封装胶的封装应力。显然,当外框宽度远大于敏感结构厚度时,满足条件2)中的刚度要求。如图 2(a)所示,由于外框的刚度远大于敏感结构刚度,芯片在承受封装应力时,外框基本上分担全部的封装应力并产生形变,而敏感结构由于刚度太小不分担封装应力,仅根据外框的形变产生向内或向外的位移。简化物理模型如图 2(b)所示,其中M为支撑梁对指针产生的转矩,Wb为支撑梁宽度,lp为指针长度,wp为指针宽度。结合式(1),推导出应力放大结构的第一级放大率:
 |
| Fig.2 Deformation and movement in stress magnifying structure, and simplified physic model of probe 图 2 放大设计模型中芯片上的形变和位移、指针简化物理模型 |
| ${\eta _1} = \frac{{{\sigma _{\rm{f}}}}}{{{\sigma _{\rm{o}}}}} = \frac{{{A_{\rm{o}}}}}{{{A_{\rm{f}}}}} = \frac{{{t_{\rm{c}}}{W_{\rm{o}}}}}{{2{t_{\rm{c}}}{W_{\rm{f}}}}} = \frac{{{W_{\rm{o}}}}}{{2{W_{\rm{f}}}}}$ | (2) |
式中:tc表示芯片的厚度;Wo与Wf分别表示原始芯片与外框的横截面宽度。第一级放大实质上是通过减小芯片上承载封装力的有效横截面积来实现应力的放大,这与材料学规律相吻合。
图 2展示了外框的形变通过支撑梁传递到指针的过程,指针横向形变量Δlp与外框形变量Δlf关系为:
| $\Delta {l_{\rm{p}}} = \Delta {l_{\rm{f}}}$ | (3) |
根据胡克定律,外框上形变与应力关系为:
| $\Delta {l_{\rm{f}}} = L{\varepsilon _{\rm{f}}} = \frac{{\left( {1 - \nu } \right)L{\sigma _{\rm{f}}}}}{E}$ | (4) |
式中:εf表示外框上的应变;E为硅的杨氏模量;ν为硅的泊松常数。
前提条件3)保证了支撑梁能够将外框形变转化为位移并传递给指针,使指针能完全根据外框的形变产生变形和应力集中。支撑梁的运动和变形主要受外框和指针影响:外框的形变推动支撑梁横向运动,而指针则导致支撑梁产生纵向运动和变形。那么,要实现支撑梁只做横向平移运动,就需要减小指针对支撑梁的影响,即增大支撑梁和指针的刚度差异。当支撑梁刚度远大于指针时,它就能几乎不受指针变形的影响,近似看作一端自由的悬臂梁,在外框形变的推动下进行横向的平移,促使指针产生变形和应力集中。显然,当支撑梁宽度远大于指针宽度时,满足条件3)中的刚度要求。将指针的变形情况进行简化,如图 3所示,其中Fb表示从支撑梁输入到指针的力,θ表示指针的偏转角。图 3展示了指针的受力与形变情况,在简化物理模型中,指针视为一端固定的悬臂梁,另一端则由支撑梁施加推力,从而产生变形。根据材料学规律,可以得到指针中的应力和形变关系为:
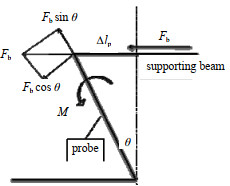 |
| Fig.3 Diagram of force and deformation analysis of probe structure 图 3 指针结构受力与形变示意图 |
| $\left\{ \begin{gathered} \Delta {l_{\rm{p}}} = \frac{{\left( {1 - \nu } \right)M{l_{\rm{p}}}^2}}{{2EI}} \\ \\ M{l_{\rm{p}}} = {F_{\rm{b}}}\cos \theta \\ \\ {\sigma _{{\rm{pm}}}} = \frac{{{F_{\rm{l}}}}}{{{A_{\rm{l}}}}} + \frac{M}{I} \cdot \frac{{{w_{\rm{p}}}}}{2} = \frac{{{F_{\rm{b}}}\sin \theta }}{{t{w_{\rm{p}}}}} + \frac{M}{I} \cdot \frac{{{w_{\rm{p}}}}}{2} \\ \end{gathered} \right.$ | (5) |
式中:I表示指针结构在指针长度方向的极矩;σpm为指针上最大应力值(位于指针根部);t为敏感结构(指针和支撑梁)的厚度;Fl与Al分别表示指针上长度方向受力与横截面积。考虑到硅材料的热膨胀系数(约2.9×10-6 ℃-1)很小,封装工艺的温度变化不大(环氧树脂胶封装温度一般为−40~60 ℃),实际上芯片的热膨胀形变很小,从而指针的变形量也很小,即偏转角度θ近似为零。结合式(3)~(5),推导出应力放大结构第二级放大率为:
| ${\eta _2} = \frac{{{\sigma _{{\rm{pm}}}}}}{{{\sigma _{\rm{f}}}}} \approx \frac{{Lw}}{{{l_{\rm{p}}}^2}}$ | (6) |
结合式(2)与式(6),推导出应力放大设计的总体应力放大率近似计算公式如下:
| $\eta = \frac{{{\sigma _{{\rm{pm}}}}}}{{{\sigma _{\rm{o}}}}} = \frac{{{\sigma _{{\rm{pm}}}}}}{{{\sigma _{\rm{f}}}}} \times \frac{{{\sigma _{\rm{f}}}}}{{{\sigma _{\rm{o}}}}} = {\eta _1}{\kern 1pt} {\eta _2} = \frac{{{W_{\rm{o}}}L{w_{\rm{p}}}}}{{2{W_{\rm{f}}}l_{\rm{p}}^2}}$ | (7) |
式中η表示应力放大率,含义为应力放大设计中指针上的最大集中应力与原始封装模型中芯片上的平均封装应力的比值。相应地,待测封装应力计算公式为:
| ${\sigma _{\rm{o}}} = \frac{{{\sigma _{{\rm{pm}}}}}}{\eta } = {\sigma _{{\rm{pm}}}} \times \frac{{2{W_{\rm{f}}}l_{\rm{p}}^2}}{{{W_{\rm{o}}}L{w_{\rm{p}}}}}$ | (8) |
式(8)中的指针最大应力σpm可由激光拉曼光谱法获得,用于计算待测封装应力。后文将针对一款高精确度MEMS微加速度计的封装应力对本文提出的测量方法进行仿真和实验验证。
2 仿真分析与讨论为了验证前文的理论分析,采用3D FEM对一款高精确度微加速度计的封装应力测量进行了仿真实验,对比了其中封装应力直接仿真结果和使用本文测量方法的仿真结果。仿真实验主要模拟了芯片的封装温度场变化过程,即芯片-胶-基底系统的温度变化(由高温固化恢复到室温),并观察芯片上指针的应力情况。
封装应力产生于微加速度计芯片下极板中,因此以芯片下极板-封装胶-基底建立原始封装模型。芯片下极板总体尺寸为长4 000 μm,宽3 000 μm,厚度400 μm。应力放大结构的芯片总体尺寸与封装模型相同,满足前提条件1)的要求;其敏感结构厚度为20 μm,外框宽度为400 μm,满足前提条件2)中外框刚度远大于敏感结构刚度的要求;敏感结构中支撑梁宽度为400 μm,指针宽度为20 μm,满足前提条件3)中支撑梁刚度远大于指针刚度的要求。指针长度为40 μm,代入式(7)计算出其理论放大率为187倍。此外,原始封装模型和应力放大结构封装模型封装应力仿真所使用的封装条件相同:封装胶厚为10 μm,四点布胶,材料为环氧树脂胶;封装温度变为60 ℃到20 ℃,基底为陶瓷材料。
图 4和图 5分别为原始封装模型和应力放大结构封装模型的有限元仿真结果。通过有限元分析计算出微加速度计下极板原始封装应力平均大小约为0.31 MPa,为压应力。而经过应力放大结构放大后,其指针上最大残余应力约53.3 MPa,同样是压应力,集中在指针根部,代入式(8)计算得待测封装应力平均值为0.285 MPa。对比封装应力直接仿真结果和使用本文测量方法的仿真结果,二者误差为8%,吻合度很高,证明本文提出的测量方法在仿真上具有可信度。
 |
| Fig.4 FEM result of residual stress of original package model 图 4 原始封装模型参与应力仿真结果 |
 |
| Fig.5 Stress distribution on probe of stress magnifying structure by FEM 图 5 应力放大结构指针上应力分布仿真结果 |
为了验证封装应力测量方法的可行性,本文针对前文所述的一款高精确度微加速度计进行了封装应力测量实验,目的是通过本文提出的测量方法测量其芯片下极板中的平均封装应力大小。
实验首先完成了对应力放大结构的测量样片的工艺设计和制作,接着进行封装和指针上最大应力的测量,最后根据式(8)计算待测MEMS微加速度计中的封装应力。
3.1 测量样片工艺设计根据前文的仿真分析,设计了样片的尺寸,使用SOI硅片和干法刻蚀工艺加工出芯片,其工艺设计如图 6所示,共分6步:1)选择厚度分布为20-0.5-380 μm的SOI硅片;2)高温氧化处理在正反两面生成氧化硅掩膜;3)使用干法刻蚀在正面刻蚀出敏感结构的形状;4)去除氧化硅掩膜,在背面溅射一层Al掩膜;5)背面进行深度干法刻蚀;6)去除Al掩膜和SOI的氧化硅层,完成应力放大结构芯片制作。芯片工艺完成后的SEM图如图 7所示。由于现实工艺限制,应力放大结构的制作工艺过程无法避免工艺尺寸误差,但尺寸误差可以通过光学显微镜进行测量并对应力放大率进行修正,例如指针的长度、宽度,支撑梁宽度,外框宽度以及芯片整体尺寸。芯片加工完成后通过光学显微镜对其关键尺寸进行了测量,设计尺寸与实际尺寸对比如表 1所示。代入式(7),计算出样片1的放大率为186倍,样片2放大率为185倍,样片3的放大率为187倍。
 |
| Fig.6 Process design of sample chip 图 6 测量样片芯片工艺设计 |
 |
| Fig.7 SEM of stress magnifying structure 图 7 应力放大结构电镜图 |
| 表 1 样片尺寸的设计值与实测值对比 Table 1 Comparison between design and measurement of dimensions of samples |
应力测量实验主要包括了对SOI硅片、应力放大结构芯片封装前后的应力测量,其中SOI硅片经过激光拉曼光谱仪测量,其拉曼峰值位置为519.797 cm-1。
样片工艺完成后,立即对所有芯片样片进行拉曼光谱测试,测量芯片指针上的拉曼光谱峰值;随后对样片进行封装,所使用的封装胶为环氧树脂胶,采用四点贴片方式布胶,固化温度为60 ℃,固化保持时间为2 h,固化完成后恢复至实验室室温20 ℃。封装完成后的实验样片如图 8所示,通过测量,封装胶厚度约为9 μm。
 |
| Fig.8 Sample of stress magnifying structure after package 图 8 应力放大结构封装样片 |
拉曼光谱仪被用于测量封装前后的实验样片指针上的最大应力值,例如图 9所示分别为样片1#封装前后的拉曼光谱测量结果。利用拉曼光谱应力测量的原理,计算各样片残余应力结果如表 2所示。表 2的结果表明,芯片封装前存在大小为30~35 MPa的拉应力,其来源为芯片制作的工艺过程,由于采用了SOI硅片,在进行高温氧化时由于氧化硅层和硅层的热失配会产生内应力。氧化硅热膨胀系数较小,故而在高温恢复常温过程中会在芯片中产生拉应力。
 |
| Fig.9 Raman spectra of sample 1# before and after package 图 9 实验样片1#封装前后的拉曼光谱 |
| 表 2 各样片的拉曼频移与残余应力 Table 2 Raman frequency shift and residual stress of samples |
显然,表 2中所测得的样片封装后残余应力应当是芯片制作工艺内应力和封装应力叠加的复合应力,对于封装产生的应力,根据前文理论分析,其性质为压应力,因此封装应力与工艺应力会进行一定程度的抵消,即实际测量值
| ${\sigma _{{\rm{package}}}} = {\sigma _{{\rm{measure}}}} - {\sigma _{{\rm{fabrication}}}}$ | (9) |
根据式(9)可以计算出被测样片中实际的封装应力大小,该封装应力为经过本文测量方法放大后的应力,将其代入式(8)计算得到微加速度计中实际的封装应力,各样片的计算结果如表 3所示。表 3表明微加速度计中平均封装应力实际大小约为0.3~0.34 MPa,为压应力,与仿真结果(0.31 MPa)相比,其测量误差低于8%,具有很高吻合度,验证了本文所提出的测量方法的可靠性。
| 表 3 封装应力测量结果与误差 Table 3 Results and errors of package residual stress measurement |
针对超低封装应力测量的问题,本文提出了一种融合显微拉曼光谱和在片应力放大结构的方法,运用应力放大关系式能够较为准确地计算出原始MEMS器件的封装应力值。针对封装应力的特点,本文提出了一种新型的两级放大结构设计,基于应力放大结构的设计原则,推导出应力放大测量所必需的应力放大关系。随后针对一款高精确度MEMS微加速度计的封装应力测量,本文成功实现了测量方法中所需应力放大结构的工艺制作,最后测量出其中下极板中平均封装应力大小,实验结果与仿真分析吻合度较高,测量误差低于8%。相比于目前常用的应力测量方法,本文的测量方法在用于测量MEMS封装应力时具有更高的精确度,成功实现了测量。
本文提出的基于在片应力放大结构和显微拉曼光谱法的超低值封装残余应力测量方法,通过改变应力放大结构参数即可以适用于不同的被测应力范围,能够对于目前的MEMS封装应力研究提供一个有效的定量测试手段,对于研究封装应力对MEMS系统的影响以及其长期稳定性提供了最直接的应力观测。然而,本文提出的测量方法只能够测量出MEMS器件中封装残余应力的平均水平,但封装应力往往是分布不均的,这是本方法的不足之处,也是未来的研究工作中值得讨论的问题。
| [1] |
吴慧, 段宝明, 秦盼, 等. 粘片工艺对MEMS器件应力的影响研究[J]. 新技术新工艺, 2016(6): 46-51. (WU Hui, DUAN Baoming, QIN Pan, et al. Research on the impact of die attach process on MEMS device stress[J]. New Technology & New Process, 2016(6): 46-51.) |
| [2] |
WALWADKAR S S, CHO J. Evaluation of die stress in MEMS packaging: experimental and theoretical approaches[J]. IEEE Transactions on Components & Packaging Technologies, 2006, 29(4): 735-742. |
| [3] |
WALWADKAR S S, CHO J, FARRELL P W, et al. Tailoring of stress development in MEMS packaging systems[C]// Materials Research Society Symposium Proceedings. Materials Research Society, 2003(741): 139-144.
|
| [4] |
PENG P, ZHOU W, YU H, et al. Investigation of the thermal drift of MEMS capacitive accelerometers induced by the overflow of die attachment adhesive[J]. IEEE Transactions on Components Packaging & Manufacturing Technology, 2017, 6(5): 822-830. |
| [5] |
YADAV I, DUTTA S, KATIYAR A, et al. Evolution of residual stress in benzocyclobutene films with temperature[J]. Materials Letters, 2015(158): 343-346. |
| [6] |
戴强, 苏伟, 张德, 等. 三明治型微加速度计温度漂移封装胶关系研究[J]. 太赫兹科学与电子信息学报, 2015, 13(1): 169-173. (DAI Qiang, SU Wei, ZHANG De, et al. Relationship between temperature drift and adhesive of sandwich type micro-accelerometers[J]. Journal of Terahertz Science and Electronic Information Technology, 2015, 13(1): 169-173.) |
| [7] |
XIN Z, PARK S, JUDY M W. Accurate assessment of packaging stress effects on MEMS sensors by measurement and sensor–package interaction simulations[J]. Journal of Microelectromechanical Systems, 2007, 16(3): 639-649. |
| [8] |
GRIESELER R, KLAUS J, STUBENRAUCH M, et al. Residual stress measurements and mechanical properties of AlN thin films as ultra-sensitive materials for nanoelectromechanical systems[J]. Philosophical Magazine, 2012, 92(25-27): 3392-3401. |
| [9] |
PABST O, SCHIFFER M, OBERMEIER E, et al. Measurement of Young's modulus and residual stress of thin SiC layers for MEMS high temperature applications[J]. Microsystem Technologies, 2012, 18(7-8): 945-953. |
| [10] |
KILINC Y, UNAL U, ALACA B E. Residual stress gradients in electroplated nickel thin films[J]. Microelectronic Engineering, 2015(134): 60-67. |
| [11] |
TAMURA N, CELESTRE R S, MACDOWELL A A, et al. Submicron X-ray diffraction and its applications to problems in materials and environmental science[J]. Review of Scientific Instruments, 2002, 73(3): 1369-1372. |
| [12] |
BANDI T, DOMMANN A, NEELS A. Analysis of stress in silicon-based microsystems by X-ray diffraction techniques[C]// Microelectronics Packaging Conference. Grenoble, France: IEEE, 2014.
|
| [13] |
LIEBOLD C, MË LLER W H. Strain maps on statically bend (001) silicon microbeams using AFM-integrated Raman spectroscopy[J]. Archive of Applied Mechanics, 2015, 85(9-10): 1353-1362. |
| [14] |
STARMAN L A, JR R A C. Using micro-Raman spectroscopy to assess MEMS Si/SiO2 membranes exhibiting negative spring constant behavior[J]. Experimental Mechanics, 2013, 53(4): 593-604. |
| [15] |
PILUSO N, ANZALONE R, CAMARDA M, et al. Micro-Raman analysis and finite element modeling of 3 C‐SiC microstructures[J]. Journal of Raman Spectroscopy, 2013, 44(2): 299-306. DOI:10.1002/jrs.4171 |
| [16] |
DUTTA S, SAXENA G, SHAVETA, et al. Comparison of residual stress in deep boron diffused silicon (100), (110) and (111) wafers[J]. Materials Letters, 2013(100): 44-46. |
| [17] |
MIYATAKE T, PEZZOTTI G. Tensor-resolved stress analysis in silicon MEMS device by polarized Raman spectroscopy[J]. Physica Status Solidi (a), 2011, 208(5): 1151-1158. |
| [18] |
STARMAN L A, LOTT J A, AMER M S, et al. Stress characterization of MEMS microbridges by micro-Raman spectroscopy[J]. Sensors and Actuators A: Physical, 2003, 104(2): 107-116. |
| [19] |
ZHAO C, LI M, YIN M, et al. Micro-Raman spectroscopy analysis of residual stress in polysilicon MEMS resonators[C]// IEEE International Conference on Nano/micro Engineered & Molecular Systems. Suzhou, China: IEEE, 2013.
|
| [20] |
VAN DRIEËNHUIZEN B P, GOOSEN J F L, FRENCH P J, et al. Comparison of techniques for measuring both compressive and tensile stress in thin films[J]. Sensors & Actuators A: Physical, 1993(37-38): 756-765. |
| [21] |
ANZALONE R, D'ARRIGO G, CAMARDA M, et al. Advanced residual stress analysis and FEM simulation on heteroepitaxial 3CSiC for MEMS application[J]. Journal of Microelectromechanical Systems, 2011, 20(3): 745-752. |
| [22] |
ERICSON F, GREEK S, SÖDERKVIST J, et al. High-sensitivity surface micromachined structures for internal stress and stress gradient evaluation[J]. Journal of Micromechanics and Microengineering, 1997, 7(1): 30-36. |
| [23] |
LIN L, PISANO A P, HOWE R T. A micro strain gauge with mechanical amplifier[J]. Journal of Microelectromechanical Systems, 1997, 6(4): 313-321. |
| [24] |
HE Q, LUO Z X, CHEN X Y. Comparison of residual stress measurement in thin films using surface micromachining method[J]. Thin Solid Films, 2008, 516(16): 5318-5323. |
 2020, Vol. 18
2020, Vol. 18


