b. 桂林电子科技大学计算机与信息安全学院,广西 桂林 541004;
c. 桂林电子科技大学信息与通信学院,广西 桂林 541004
b. School of Computer Science and Information Security, Guilin University of Electronic Technology, Guilin Guangxi 541004, China;
c. School of Information and Communication Engineering, Guilin University of Electronic Technology, Guilin Guangxi 541004, China
雷达距离的高分辨力可以通过发射大带宽的信号来实现,而角度的高分辨需要增加天线孔径来实现。基于此,多输入多输出(MIMO)雷达体制被认为是增加天线孔径的一项重要技术[1]。MIMO雷达主要有频分复用(Frequency Division Multiplexing,FDM)、码分多路复用(Code Division Multiplexing,CDM)和时分复用(TDM)几种实现形式。考虑到实现复杂度及半导体器件成本限制,基于TDM-MIMO技术的毫米波雷达已经得到广泛应用,成为智能汽车必不可少的传感器之一。本文所示的TDM-MIMO雷达采用了调频连续波(FMCW)信号,其发射信号是实时正交的。每帧由多个块组成,每个块由多个发射天线(TX)交替发射的波形组成。TDM-MIMO是从多个发射天线中分离信号的最简单方法,通常情况下,发射天线的间距是接收天线的N倍。并且TDM-MIMO系统形成的虚拟阵列相当于一个单输入多输出(Single Input Multi Output,SIMO)系统,可以实现相同的角度分辨力[2]。目前,TDM-MIMO仍存在一些缺陷,主要体现为:首先,由于TDM本身的体制特点,系统在慢时间维的采样率有所降低,使得不模糊测速范围显著减小,测速模糊出现的概率增大,最终增大角度测量误差,为了解决这种问题,已有学者提出了相应的解速度模糊方法[3-4]。其次,在不同的发射天线切换时间内,运动目标的多普勒频率引起的相位变化将耦合到各个虚拟接收天线上,从而影响接收虚拟天线孔径的正确合成,导致虚拟阵列出现散焦效应。这种相位变化会对目标的角度估计产生影响。因此,对于TDM-MIMO雷达来说,运动目标在进行角度估计之前进行相位补偿是必不可少的一部分。
国内外机构对TDM-MIMO雷达的相位补偿进行了一系列相关研究。文献[5]中,Feger R等最早提出采用TDM技术实现发射波形正交的FMCW的MIMO雷达,并设计了收发一体的阵列天线,这种阵列天线会产生冗余的虚拟位置,通过对这2个处于相同位置的虚拟天线接收的信号进行比较得出运动引入相位差,从而进行补偿。但是这种收发一体的天线相互之间的影响较大,会引起天线方向图的畸变,需要较高的隔离度。文献[6]在文献[5]的基础上,将发射与接收天线分离,同样利用虚拟阵列天线的冗余阵元比较求得相位差进行补偿。但是这种方法同样减小了虚拟天线阵列的有效孔径,从而使角度分辨率降低。文献[7]提出了使用单天线通道信号探测目标,并计算目标的运动速度,从而计算运动引入的相位差。但是这种单通道的目标探测方式,会使小信噪比较低的目标淹没在噪声中,从而造成目标的相位差项匹配失调。文献[8]描述的另一种方法是通过频率斜坡的交错传输来减少误差。文献[9]通过优化发射天线的切换方案来减少相位误差。文献[10]提出了一种基于随机传输方案应用稀疏重构重建目标多普勒频谱的运动补偿方法。在该方法中速度与角度不再是耦合的。文献[11]设计了一种交替发射的信号调制方案,用以补偿速度产生的耦合相变。文献[12]在对信号提出了一种新的求离散傅里叶变换的方法,用来对相位误差项进行消除,这种方法无需预估目标速度,并且可以使用多目标的情况。
1 TDM-MIMO信号模型雷达系统采用线性调制的FMCW信号见图 1,因此发射天线的时变正弦信号
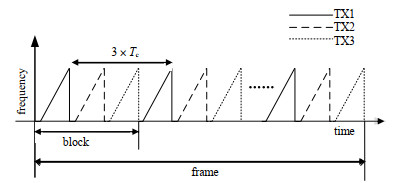 |
| Fig.1 TDM-MIMO transmit waveform 图 1 TDM-MIMO发射波形 |
| $f[n] = {f_0} + \frac{B}{N}n$ | (1) |
式中:
假设目标位于远场,无噪声环境下,对于静止目标,接收端的中频信号
| $s[n] = AG(\alpha )\exp \left\{ {{\rm{j}}\left[ {2{\rm{ \mathsf{ π} }}f[n]\frac{{2r}}{c} + {\phi _{{\rm{refl}}}}} \right]} \right\}$ | (2) |
式中:A为信号的幅度值;
TDM-MIMO雷达虚拟阵列见图 2,将经过发射天线(TX)→目标→接收天线(RX)进行传播,信号时延由3部分组成:
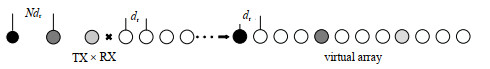 |
| Fig.2 Equivalent virtual array of TDM-MIMO radar 图 2 TDM-MIMO雷达的等效虚拟阵列 |
1) 雷达与目标径向距离造成的时延:
2) 由发射天线
3) 由接收天线
因此可以得出:
| ${s_{{\rm{MIMO}}}}\left[ {n, {m_{\rm{t}}}, {m_{\rm{r}}}} \right] = s[n]\exp \left( {{\rm{j}}2{\rm{ \mathsf{ π} }}f[n]{\tau _{\rm{t}}}[{m_{\rm{t}}}]} \right)\exp \left( {{\rm{j}}2{\rm{ \mathsf{ π} }}f[n]{\tau _{\rm{r}}}[{m_{\rm{r}}}]} \right)$ | (3) |
式中:
综上,完整的TDM-MIMO中频信号模型为:
| ${s_{{\rm{MIMO}}}}\left[ {n, {m_{\rm{t}}}, {m_{\rm{r}}}} \right] = \underbrace {A\exp \left\{ {{\rm{j2 \mathsf{ π} }}\frac{{{f_0}}}{c}\sin \;\alpha ({d_{\rm{t}}}[{m_{\rm{t}}}] + {d_{\rm{r}}}[{m_{\rm{r}}}])} \right\}}_a\underbrace {\exp \left( {{\rm{j4 \mathsf{ π} }}\frac{B}{{Nc}}rn} \right)}_b\underbrace {\exp \left[ {{\rm{j}}4{\rm{ \mathsf{ π} }}\frac{{{f_0}}}{c}r + {\phi _{{\rm{refl}}}}} \right]}_c$ | (4) |
目前为止,雷达系统均是基于静态目标的信号模型实现,未将可能的目标移动考虑在内,需要对信号模型进行一些扩展。在远场条件下,目标相对于目标坐标系的位移引起最大允许相位误差通常为
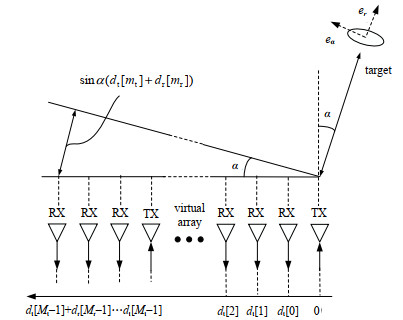 |
| Fig.3 Signal model of TDM-MIMO equivalent virtual array 图 3 TDM-MIMO等效虚拟阵列信号模型示意 |
1) 目标在
2) 目标在
目前道路上汽车的行驶速度不会超过70 m/s,因此对于77 GHz TDMA–MIMO雷达,由目标径向运动引起的c部分的相位变化造成的影响最为关键[5]。将这部分多普勒频移考虑到信号模型中,则新的运动单目标信号模
型[6]为:
| ${s_{{\rm{MOVE - MIMO}}}}[n, {m_{\rm{t}}}, {m_{\rm{r}}}] = {s_{{\rm{MIMO}}}}[n, {m_{\rm{t}}}, {m_{\rm{r}}}] \times \exp ({\rm{j}}2{\rm{ \mathsf{ π} }}\psi n)$ | (5) |
式中:
考虑多目标的情况,其信号模型为:
| $s\left[ {n, {m_{\rm{t}}}, {m_{\rm{r}}}} \right]{\rm{ = }}\sum\limits_{k = 1}^K {{A_k}\exp \left\{ {{\rm{j}}2{\rm{ \mathsf{ π} }}\frac{{{f_0}}}{c}\sin \;{\alpha _k}({d_{\rm{t}}}[{m_{\rm{t}}}] + {d_{\rm{r}}}[{m_{\rm{r}}}])} \right\}\exp ({\rm{j}}4{\rm{ \mathsf{ π} }}\frac{B}{{Nc}}{r_k}n)\exp \left[ {{\rm{j}}(4{\rm{ \mathsf{ π} }}\frac{{{f_0}}}{c}{r_k} + {v_{r - k}}{T_{\rm{s}}}n) + {\phi _{{\rm{refl}}}}} \right]} $ | (6) |
式中:
对TDM-MIMO雷达系统来说目标的相对运动会带来散焦效应,使能量分布在整个角度范围内,无法正确进行角度测量,因此必须对目标运动引起的相位变化进行补偿矫正,使其重新聚焦。
2 相位补偿方法对每个发射天线(TX)对应的接收天线(RX)中频回波信号进行采样,单周期采样点数为N,啁啾的重复周期数为I,此时可将可测量距离分为N个距离单元,可测量速度分为I个速度单元,由此可以得到对应的距离分辨力和速度分辨力:
| $S\left( {n, i, {m_{\rm{t}}}, {m_{\rm{r}}}} \right) = \sum\limits_{i = 0}^{I - 1} {\sum\limits_{n = 0}^{N - 1} {{s_i}[n, {m_{\rm{t}}}, {m_{\rm{r}}}]} } \exp \left( {\frac{{ - {\rm{j2 \mathsf{ π} }}{n^2}}}{N}} \right)\exp \left( {\frac{{ - {\rm{j2 \mathsf{ π} }}{i^2}}}{I}} \right)$ | (7) |
式中
每个2D-FFT频谱矩阵对应一个虚拟天线,为了提高信噪比,将所有虚拟天线的频谱进行非相干累加。然后,使用恒虚警算法(Constant False-Alarm Rate,CFAR)从2D-FFT频谱中筛选出有效目标的峰值。在进行角度估计之前先对速度引起的相位变化进行补偿。根据式(6)可以看出,对于TDM-MIMO雷达系统,除了第一顺位的发射天线(TX1)与其对应的接收天线的回波信号之外的回波信号,均需以TX1为标准,对相应的回波信号进行相位补偿。根据速度引起的多普勒频移
| $S{\rm{'(}}{m_{\rm{t}}}{\rm{, }}{m_{\rm{r}}}{\rm{) = }}S({m_{\rm{t}}}{\rm{, }}{m_{\rm{r}}}{\rm{)}}\exp \left[ { - {\rm{j2 \mathsf{ π} }}{f_D}{T_c}\left( {\frac{{{m_{\rm{t}}} - 1}}{{{M_t}}}} \right)} \right]$ | (8) |
式中:
| $S'({m_{\rm{t}}}, {m_{\rm{r}}}) = S({m_{\rm{t}}}, {m_{\rm{r}}}){\rm{exp}}\left( {\frac{{ - {\rm{j}}2{\rm{ \mathsf{ π} }}{m_{\rm{t}}}i}}{{{M_{\rm{t}}}I}}} \right){\rm{, }}\quad 0 \leqslant i \leqslant I - 1$ | (9) |
使用式(9)对2D-FFT之后速度单元进行补偿。在进行多普勒补偿之后,对于每个有效目标,从12个2D-FFT频谱中提取对应峰值单元,并在补零之后执行角度-FFT。这里补零的目的是为了细化频谱,从而更准确地找到目标的谱峰位置,以确定该目标的到达角。
在雷达信号处理过程中加入本文提出的基于速度单元的相位补偿方法可以正确地对相位进行矫正,进而可以正确地对运动目标进行角度测量。从式(9)中可以看出,雷达速度分辨力是影响本文提出方法性能的关键所在,也就是说,在调频周期
本文仿真的TDM-MIMO雷达系统,具有3个发射天线(间距
| 表 1 发射波形参数 Table 1 Parameters of transmit waveform |
为了证明本文中提出的对运动多普勒相位补偿方法的有效性,首先设计仿真实验针对处于不同运动状态下的目标进行角度测量,角度测量方法分为直接对多天线2D-FFT频谱的有效峰值执行角度-FFT和对多天线的2D-FFT频谱进行相位补偿之后再对有效峰值进行角度-FFT。考虑运动目标在相对雷达的多个方向上的情况,其仿真结果见表 2。
| 表 2 多角度仿真结果 Table 2 Multi-angle simulation results |
由表 2可以看出对细化之后的频谱执行角度-FFT的测角结果,具有较高的准确度。当被测目标在运动时,直接测角的方法会因为散焦效应而失效,出现将一个目标认为是多个目标或者测角偏差较大的情况。在经过本文的相位补偿方法处理之后,可以正确地得到与目标静止时相同的角度信息。由于傅里叶变换具有可加性,本方法同样适用于多目标的情况。
3.2 相位补偿方法对比为了验证算法的准确性及高效性,仿真了1TX-12RX的SIMO雷达系统,这种情况无需进行相位补偿。并且仿真了3TX-4RX的TDM-MIMO的雷达系统,分别使用文献[6]中的重复阵元方法进行相位补偿以及本文中提出的方法进行相位补偿。仿真被测目标径向距离为10 m,径向速度为10 m/s,角度为–20°。3种方法的角度峰值见图 4,2种补偿后的方法的测角结果与SIMO雷达系统的直接测角结果均为–18.28°。对比可以看出使用重复阵元补偿的方法,峰值较宽,并且峰值旁瓣较高。这是因为天线孔径的减少影响了角度分辨力;而使用本文提出的方法峰值较尖锐,并且旁瓣曲线与SIMO雷达系统走向大致相同。可以看出本文提出的方法具有准确性。
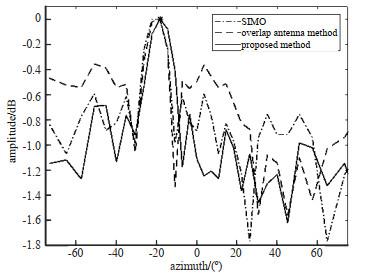 |
| Fig.4 Spatial spectrum of different methods 图 4 不同方法的空间谱 |
对以上3种情况分别进行多次实验并记录信号处理算法的完整运行时间,实验结果见图 5,使用重复阵元方法补偿和使用本文方法补偿的平均耗时分别为0.011 1 s和0.011 3 s,未进行相位补偿的平均耗时为0.010 8 s。可以看出3种方法的耗时在一个数量级,具有相同的时间复杂度。因此本文提出的相位补偿方法同样具有高效性。
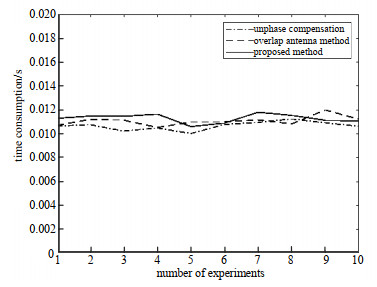 |
| Fig.5 Signal processing time for different methods 图 5 不同方法的信号处理时间 |
为进一步验证本文方法在实际雷达系统中的可行性,使用德州仪器(Texas Instruments)的AWR1243EVM+ DCA1000EVM在雷达模拟器中采集目标的原始回波数据,将采集到的原始数据使用PC进行实验。AWR1243EVM具有3个发射天线(间距
 |
| Fig.6 Data acquisition 图 6 数据采集场景 |
使用雷达模拟器产生雷达截面积为10 dBsm的目标,该目标沿着0°方向上以20 m/s的速度,从距离雷达10 m的位置运动到30 m的位置。对采集到的中频信号按照第2节中描述的算法流程进行信号处理,取其中的一帧数据得出未进行相位补偿时的目标距离-角度图,见图 7,单位为m。此时频谱受目标相对运动影响,角度谱峰产生了偏移,并且产生了散焦效应,无法正确估计目标的角度。使用本文提出的相位补偿方法对频谱进行补偿后得到其目标距离-角度图,见图 8,单位为m。可以看出角度谱峰回到了正确的位置,并且起到了重新聚焦的效果。再次证明了本文提出的相位补偿方法能够校正目标运动引起的相位偏移。
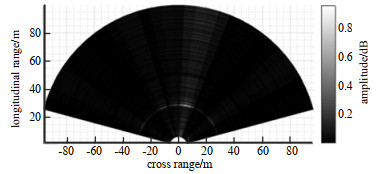 |
| Fig.7 Distance-angle plot without compensation 图 7 未补偿时距离-角度图 |
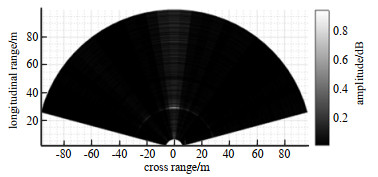 |
| Fig.8 Distance-angle plot after compensation 图 8 补偿后距离-角度图 |
本文基于目标运动的TDM-MIMO信号模型,提出了相位补偿的方法,使得虚拟阵列天线的孔径能够正确合成。本文提出的基于速度单元的相位补偿方法可以应用于多目标场景,并且不受测速精确度的影响,无需额外的硬件开销。通过仿真实验和实测数据验证了本方法可以使运动目标正常测角并且具有较低的时间复杂度。
| [1] |
BLISS D W, FORSYTHE K W. Multiple-input Multiple-Output(MIMO) radar and imaging: degrees of freedom and resolution[C]// Conference Record of the Thirty-Seventh Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA, USA: IEEE, 2003: 54-59. http://www.researchgate.net/publication/4071761_Multiple-input_multiple
|
| [2] |
ZWANETSKI A, ROHLING H. Continuous wave MIMO radar based on time division multiplexing[C]// 13th International Radar Symposium. Warsaw, Poland: IEEE, 2012: 119-121. http://www.researchgate.net/publication/254043258_Continuous_wave_MIMO_radar_based_on_time_division_multiplexing
|
| [3] |
ROOS F, BECHTER J, APPENRODT N, et al. Enhancement of Doppler unambiguity for chirp-sequence modulated TDM- MIMO radars[C]// MTT-S International Conference on Microwaves for Intelligent Mobility. Munich, Germany: IEEE, 2018. DOI: 10.1109/ICMIM.2018.8443352.
|
| [4] |
郑远, 温博, 马瑞平. 基于双周期锯齿波LFMCW的距离速度去耦合[J]. 电子科技, 2013, 26(7): 125-128. (ZHENG Yuan, WEN Bo, MA Ruiping. Range-velocity decoupling based on dual period sawtooth wave LFMCW radar[J]. Electronic Science and Technology, 2013, 26(7): 125-128. DOI:10.3969/j.issn.1007-7820.2013.07.038) |
| [5] |
FEGER R, WAGNER C, SCHUSTER S, et al. A 77 GHz FMCW MIMO radar based on an SiGe single-chip transceiver[J]. IEEE Transactions on Microwave Theory and Techniques, 2009, 57(5): 1020-1035. DOI:10.1109/TMTT.2009.2017254 |
| [6] |
SCHMID C M, FEGER R, PFEFFER C, et al. Motion compensation and efficient array design for TDMA FMCW MIMO radar systems[C]// 6th European Conference on Antennas & Propagation. Prague, Czech Republic: IEEE, 2012: 1746-1750. https://www.researchgate.net/publication/261229726_Motion_compensation_and_efficient_array_design_for_TDMA_FMCW_MIMO_radar_systems?_sg=EU6dfxS0aTE5LlIOb9Gc8eebe-51o4RHstoOTSqzO2F9u3gu5rdJHOv5au_6wUl_1VVs27WOhR-qF-5mwJH0SQ
|
| [7] |
ZOEKE D, ZIROFF A. Phase migration effects in moving target localization using switched MIMO arrays[C]// 2015 European Radar Conference(EuRAD). Paris, France: IEEE, 2015: 85-88. https://www.researchgate.net/publication/308734419_Phase_migration_effects_in_moving_target_localization_using_switched_MIMO_arrays
|
| [8] |
GUETLEIN J, KIRSCHNER A, DETLEFSEN J. Motion compensation for a TDM FMCW MIMO radar system[C]// 2013 European Radar Conference(EuRAD). Nuremberg, Germany: IEEE, 2013: 37-40. https://www.researchgate.net/publication/261091989_Motion_compensation_for_a_TDM_FMCW_MIMO_radar_system
|
| [9] |
RAMBACH K, YANG B. Colocated MIMO radar: Cramer-Rao bound and optimal time division multiplexing for DOA estimation of moving targets[C]// IEEE International Conference on Acoustics, Speech and Signal Processing. Vancouver, BC, Canada: IEEE, 2013: 4006-4010. https://www.researchgate.net/publication/261281981_Colocated_MIMO_radar_Cramer-Rao_bound_and_optimal_time_division_multiplexing_for_DOA_estimation_of_moving_targets
|
| [10] |
HU Xueyao, LU Man, LI Yang, et al. Motion compensation for TDM MIMO radar by sparse reconstruction[J]. Electronics Letters, 2017, 53(24): 1604-1606. DOI:10.1049/el.2017.3524 |
| [11] |
KRONAUGE M, ROHLING H. New chirp sequence radar waveform[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(4): 2870-2877. DOI:10.1109/TAES.2014.120813 |
| [12] |
BECHTER J, ROOS F, WALDSCHMIDT C. Compensation of motion-induced phase errors in TDM MIMO radars[J]. IEEE Microwave and Wireless Components Letters, 2017, 27(12): 1164-1166. DOI:10.1109/LMWC.2017.2751301 |
 2020, Vol. 18
2020, Vol. 18

