移动对移动(M2M)通信是第五代(5G)智能交通系统的一个重要研究课题。宏蜂窝M2M通信系统旨在减少交通事故,提高交通效率,促进5G移动应用的发展[1]。对于设计5G宏蜂窝M2M无线通信系统性能,研究无线信道中发射端和接收端之间的传输特性[2-3]是关键。因此,5G通信中的宏蜂窝M2M通信信道建模对实现我国在5G通信领域的战略领导地位具有重要意义。
对于无线MIMO通信环境,发射端(Tx)发出的信号在到达接收端之前会撞击路边环境中的散射体[4]。因此,采用莱斯衰落信道表征5G宏蜂窝M2M通信信道中的传播特性[5]。数值研究[6]表明,基于几何的随机信道模型(Geometry-Based Stochastic Models,GBSMs)复杂度极低,精确度很高,已被广泛用于研究5G宏蜂窝M2M信道的统计传播特性。因此,可以根据发送端、接收端和干扰对象等之间的特定几何关系,推导出不同情况下的传播路径长度和角度参数。文献[7-8]提出了多反射散射模型研究车对车(Vehicle-to-Vehicle,Ⅴ2Ⅴ)通信信道的统计特性,采用椭圆模型来描述移动无线通信环境中干扰对象的分布区域。文献[9]提出一种适用于宏蜂窝移动环境的统计几何传播模型,该模型假定传播组件从发送端到接收端有单一交互作用,同时假设对象的分布区域为均匀分布在接收端周围的一个圆内。此外,基于速度运动方向固定的假设,文献[10]研究了双环宏蜂窝M2M参考模型中宏蜂窝M2M信道的时变统计特性。文献[11]中的测量表明:当发射端和接收端在二维(2D)模型中传播时,系统性能的估计不准确,因此,使用三维(3D)信道模型,包括方位角和高程角参数,用于评估通道传播特性[12]非常必要。文献[13]提出一种用于隧道场景中Ⅴ2Ⅴ通信的三维(3D)宽带MIMO信道模型,该模型引入了许多共焦点半椭球模型来研究Ⅴ2Ⅴ信道在不同传播时延下的统计特性。文献[14]选择了一些共焦点椭圆圆柱体来描述路边环境中的散射体分布。文献[15-16]提出了三维散射信道模型,分别描述了在宏蜂窝和微蜂窝环境中的移动无线电通信特性,但文献中使用半椭球体模拟路边散射体是不合理的,因为路边散射体不可能存在于天空中。文献[17]提出一种用于窄带MIMO宏蜂窝M2M通信的三维几何多径衰落信道模型,该模型采用两圆柱模型来描述路边通信场景中建筑物的散射面。文献[18]提出了一个三维MIMO信道模型模拟空中发射端和地面接收端之间的通信,该模型介绍了位于三维倾斜椭球体模型2个焦点处的高空电子发射端和地面接收端。文献[19]提出一种宽带非平稳Ⅴ2Ⅴ随机信道模型,研究了时变信道统计特性。
上述信道模型主要适用于微蜂窝通信场景,但当发送器距离接收器较远时,即宏小区通信场景,这些模型已不再满足需要。因此本文引入MIMO信道模型来研究5G宏蜂窝M2M通信系统[20-21]。
1 系统模型在多径信道中,每个信道的传播路径长度波决定了传播时延和接收端处的波的平均功率。因此,现有的文献使用数学模型和算法进行信道建模,用来表示发送端和接收端之间的多径传播信道[22]。如图 1所示,采用三维圆柱体描述宏蜂窝M2M通信场景中有效散射体分布的信道模型。定义Tx和Rx分别配备了MT和MR个均匀线性阵列(Uniform Linear Array,ULA)天线。Tx和Rx处的两个相邻天线的间距分别表示为δT和δR。Tx和Rx处的天线阵的方位角相对于x轴正方向分别表示为ΨT和ΨR。从Tx中心点到Rx中心点的距离为D。Rx周围的圆柱面半径为Rr。假设圆柱模型表面存在N个有效散射体(即干扰物),其中第n个(n=1, 2, …, N)散射体被指定为S(n)。M2M信道中的Tx和Rx不是静态的,可以在空中和水平面任意移动。因此,Tx和Rx的移动速度分别为vT和vR,移动方向的方位角分别表示为γT和γR。
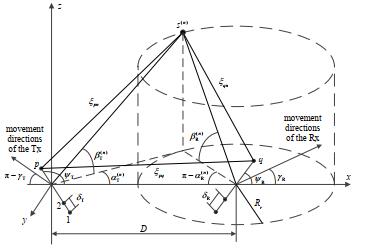 |
| Fig.1 3D cylindrical macro cellular mobile communication MIMO channel model 图 1 三维圆柱宏蜂窝移动通信MIMO信道模型 |
在所提出的宏蜂窝M2M通信信道模型中,信号从Tx经过视距分量(LoS)和非视距分量(NLoS)传播到Rx。采用矩阵H(t)=[hpq(t, τ)]MR×MT并且尺寸为MR×MT反映MIMO信道中的物理传输特性[3],其中hpq(t, τ表示第p个(p=1, 2, …, MT)发射阵列天线和第q个(q=1, 2, …, MR)接收阵列天线[23-24]的复杂信道脉冲响应(Channel Impulse Response,CIR)。因此,LoS传播分量的CIR可以表示为:
| $ h_{pq}^{{\rm{LoS}}}(t) = \sqrt {\frac{K}{{K + 1}}} {{\rm{e}}^{{\rm{j}}({\varphi _0} - 2{\rm{ \mathit{ π} }}{f_c}\xi _{pq}^{{\rm{LoS}}}/c)}} \times {{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathit{ π} }}}}{\lambda }{\upsilon _{\rm{T}}}tcos(\alpha _{\rm{T}}^{{\rm{LoS}}} - {\gamma _{\rm{T}}})cos\beta _{\rm{T}}^{{\rm{LoS}}}}} \times {{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathit{ π} }}}}{\lambda }{\upsilon _{\rm{R}}}tcos(\alpha _{\rm{R}}^{{\rm{LoS}}} - {\gamma _{\rm{R}}})cos\beta _{\rm{R}}^{{\rm{LoS}}}}} $ | (1) |
式中:φ0为非视距分量的初始相移,假设它是一个独立的随机变量,并从-π到π均匀分布,即φ0?[-π, π];k为系数;c为光速;αTLoS和αRLoS分别为LoS传播分量的方位离开角(Azimuth Angle Of Departure,AAOD)和方位到达角(Azimuth Angle Of Arrival,AAOA);βTLoS和βRLoS分别为LoS传播分量的高程离开角(Elevation Angle Of Departure,EAOD)和高程到达角(Elevation Angle Of Arrival,EAOA);ξpq为第p个发射天线直接到第q个接收天线的传播距离:
| $ {\xi _{pq}} = D - {k_p}{\delta _{\rm{T}}}\cos {\psi _{\rm{T}}} + {k_q}{\delta _{\rm{R}}}\cos {\psi _{\rm{R}}} $ | (2) |
式中:kp =(MT-2p+1)/2; kq =(MR -2q+1)/2。
当波从Tx传播到Rx时,并考虑干扰物的反射,即NLoS传播分量的CIR表示为:
| $ h_{pq}^{{\rm{NLoS}}}(t) = \sqrt {\frac{1}{{K + 1}}} \sum\limits_{n = 1}^N {\frac{1}{{\sqrt N }}} {{\rm{e}}^{{\rm{j}}({\varphi _0} - 2{\rm{ \mathit{ π} }}{f_c}[\xi _{pn}^{} + {\xi _{qn}}]/c)}} \times {{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathit{ π} }}}}{\lambda }{\upsilon _{\rm{T}}}tcos(\alpha _{\rm{T}}^{(n)} - {\gamma _{\rm{T}}})cos\beta _{\rm{T}}^{(n)}}} \times {{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathit{ π} }}}}{\lambda }{\upsilon _{\rm{R}}}tcos(\alpha _{\rm{R}}^{(n)} - {\gamma _{\rm{R}}})cos\beta _{\rm{R}}^{(n)}}} $ | (3) |
式中:αT(n)和βT(n)分别为发射端到散射体s(n)的AAOD和EAODαR(n)和βR(n)分别为接收端的AAOA和EAOA到散射体s(n)的传播路径;ζpn和ζqn分别为第p个发射天线和第q个接收天线到散射体s(n)的几何传播路径的长度,分别表示为:
| $ \begin{array}{*{20}{c}} {{\xi _{pn}} = \sec \beta _{\rm{T}}^{(n)}\left[ {{D^2} + R_r^2 + {{({k_p}{\delta _{\rm{T}}})}^2} + 2D{R_r}\cos \alpha _{\rm{R}}^{(n)} - 2\sqrt {{D^2} + R_r^2 + 2DR_r^{}\cos \alpha _{\rm{R}}^{(n)}} ) \times {k_p}{\delta _{\rm{T}}}\cos (\alpha _{\rm{T}}^{(n)} - {\psi _{\rm{T}}})} \right],}\\ { - \arcsin ({R_r}/D) \le \alpha _{\rm{T}}^{(n)} \le \arcsin ({R_r}/D)} \end{array} $ | (4) |
| $ {\xi _{qn}} = \sec \beta _{\rm{R}}^{(n)} \times \sqrt {R_{\rm{T}}^2 + {{({k_q}{d_R})}^2} + 2{R_r}{k_q}{d_{\rm{R}}}\cos (\alpha _{\rm{R}}^{(n)} - {\psi _{\rm{R}}})} ,{\rm{ }} - {\rm{\pi }} \le \alpha _{\rm{R}}^{(n)} \le {\rm{\pi }} $ | (5) |
现有的文献[25]采用了一系列散射体的闭式表达式分布,如均匀分布、高斯分布、拉普拉斯分布、冯米赛斯分布,描述AAOD, EAOD, AAOA和EAOA的角度参数。概率密度函数(Probability Density Function,PDF)的冯米赛斯分布推导如下:
| $ f({\alpha ^{(n)}}) = \frac{{{{\rm{e}}^{k\cos ({\alpha ^{(n)}} - \alpha )}}}}{{2{\rm{ \mathit{ π} }}{I_0}(k)}}, {\rm{ }}0 \le {\alpha ^{(n)}} \le 2{\rm{ \mathit{ π} }} $ | (6) |
式中:α为方位到达角的平均值;I(·)为第一类零阶修正贝塞尔函数;K(K≥0)为控制角扩散的实值参数。EAOA的余弦分布如下:
| $ f({\beta ^{(n)}}) = \frac{{\rm{ \mathit{ π} }}}{{4{\beta _0}}}cos\left( {\frac{{\rm{ \mathit{ π} }}}{2} \times \frac{{{\beta ^{(n)}} - {\beta _0}}}{{{\beta _m}}}} \right), {\rm{ }}{\beta _0} - {\beta _m} \le {\beta ^{(n)}} \le {\beta _0} - {\beta _m} $ | (7) |
式中:β0为仰角的平均值;βm为β(n)的方差。本文采用了冯米赛斯分布的闭式表达式,因为它具有描述衰落信道方位角和仰角变量的优点[26]。当Tx和Rx之间的通信处于各向同性散射时,
模型中复合信道脉冲响应hpq(t, τ)能够表示视距(LoS)传播路线和圆柱模型表面上的有效散射体反射的非视距(NLoS)传播路线的物理特性。因此,模型中两种不同传播路径的空间共因系数为:
| $ {\rho _{{h_{pq, }}{h_{p'q'}}}}(t, \tau ) = E[{h_{pq}}(t)h_{p'q'}^*(t - \tau )] $ | (8) |
式中hpq(t)和hp′q′(t)为两种不同传播路径的复合信道脉冲响应。LoS传播分量和有效散射体反射分量是相互独立的,因此,该模型中传播分量的空间互相关函数(CCF)可以表示为:
| $ {\rho _{{h_{pq, }}{h_{p'q'}}}}(t, \tau ) = \rho _{{h_{pq, {h_{p'q'}}}}}^{{\rm{LoS}}}(t, \tau ) + \rho _{{h_{pq, {h_{p'q'}}}}}^{{\rm{NLoS}}}(t, \tau ) $ | (9) |
将式(1)代入式(8)中,空间互相关函数(CCF)的视距(LoS)分量可以表示为:
| $ \rho _{{h_{pq, }}{h_{p'q'}}}^{{\rm{LoS}}}(t, \tau ) = K{{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathit{ π} }}}}{\lambda }(p - p'){\delta _{\rm{T}}}\cos {\psi _{\rm{T}}} - (q - q'){\delta _{\rm{R}}}\cos {\psi _R}}} \times {{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathit{ π} }}}}{\lambda }{\upsilon _{\rm{T}}}\tau cos(\alpha _{\rm{R}}^{{\rm{LoS}}} - {\gamma _{\rm{T}}})cos\beta _{\rm{T}}^{{\rm{LoS}}}}} \times {{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathit{ π} }}}}{\lambda }{\upsilon _{\rm{R}}}\tau cos(\alpha _{\rm{R}}^{{\rm{LoS}}} - {\gamma _{\rm{R}}})cos\beta _{\rm{R}}^{{\rm{LoS}}}}} $ | (10) |
将式(3)代入式(8)中,空间互相关函数(CCF)的非视距分量可表示为:
| $ \rho _{{h_{pq, }}{h_{p'q'}}}^{{\rm{NLoS}}}(t, \tau ) = \mathop {\lim }\limits_{N \to \infty } \sum\limits_{n = 1}^N {\frac{1}{N}} \times {{\rm{e}}^{{\rm{j}}\frac{{{\rm{2 \mathit{ π} }}}}{\lambda }\tau '[{\upsilon _{\rm{T}}}cos(\alpha _{\rm{T}}^{(n)} - {\gamma _{\rm{T}}}) - {\upsilon _{\rm{R}}}cos(\alpha _{\rm{R}}^{(n)} - {\gamma _{\rm{R}}})]}} \times {{\rm{e}}^{{\rm{j2 \mathit{ π} }}{f_c}[{\xi _{pn}} + {\xi _{qn}} - {\xi _{p'n}} - {\xi _{q'n}}]/c}} $ | (11) |
AAoA和EAoA的角度变量与有效散射体反射的成分中的AAoD和EAoD的角度变量相关。因此,基于图 1中的几何模型,几何关系表达为:
| $ \alpha _{\rm{T}}^{(n)} = \arctan \frac{{{\xi _{qn}}\cos \beta _{\rm{R}}^{(n)}\sin \alpha _{\rm{R}}^{(n)}}}{{D - {\xi _{qn}}\cos \beta _{\rm{R}}^{(n)}\cos \alpha _{\rm{R}}^{(n)}}} $ | (12) |
| $ \beta _{\rm{T}}^{(n)} = \arctan \frac{{{\xi _{qn}}\sin \beta _{\rm{R}}^{(n)}}}{{\sqrt {F_0^2{{\sin }^2}\alpha _{\rm{R}}^{(n)} + {{(D - {F_0}\cos \alpha _{\rm{R}}^{(n)})}^2}} }} $ | (13) |
式中F0=ξqncosβR(n)。
当圆柱模型表面上的散射体数量接近无穷大时,即
| $ 1/N = f({\alpha _{\rm{R}}})f({\beta _{\rm{R}}})d{\alpha _R}{\rm{d}}{\beta _{\rm{R}}} $ | (14) |
式中:f(αR)和f(βR)分别表示方位到达角和仰角变量的PDF冯米赛斯分布(式(6)和式(7))。式(11)可改写为:
| $ \rho _{{h_{pq, }}{h_{p'q'}}}^{{\rm{NLoS}}}(t, \tau ) = \int_{ - {\rm{ \mathit{ π} }}}^{\rm{ \mathit{ π} }} {\int_{ - {\rm{ \mathit{ π} }}}^{\rm{ \mathit{ π} }} {{{\rm{e}}^{{\rm{j2 \mathit{ π} }}{f_c}[{\xi _{pn}} + {\xi _{qn}} - {\xi _{p'n}} - {\xi _{q'n}}]/c}}} {{\rm{e}}^{{\rm{j}}\frac{{2{\rm{ \mathit{ π} }}}}{\lambda }\tau [{\upsilon _{\rm{T}}}cos(\alpha _{\rm{T}}^{(n)} - {\gamma _{\rm{T}}}) - {\upsilon _{\rm{R}}}cos(\alpha _{\rm{R}}^{(n)} - {\gamma _{\rm{R}}})]}}f({\alpha _{\rm{R}}})f({\beta _{\rm{R}}})d{\alpha _{\rm{R}}}{\rm{d}}{\beta _{\rm{R}}}} $ | (15) |
令参数p=p′和q=q′,可以得到所提出的模型中传播路径的时间自相关系数(ACF)的表达式:
| $ {\rho _{{h_{pq}}}}(t, \Delta t) = E[{h_{pq}}(t)h_{pq}^*(t + \Delta t)] $ | (16) |
所提出的宏蜂窝M2M信道模型中,视距传播分量和有效散射体反射分量共同影响多普勒功率谱密度的分布。无线信道中多普勒功率谱密度(PSD)的闭合形式表达式可以通过时间间隔Δt的傅里叶变换在时间ρhpq(t, Δt)表达式中表示,即:
| $ {S_{{h_{pq}}}}({f_{\rm{D}}}, t) = \int_{ - \infty }^\infty {{\rho _h}_{_{p, q}}} (t, \Delta t){e^{ - {\rm{j2 \mathit{ π} }}{f_{\rm{D}}}\Delta t}}{\rm{d}}\Delta t $ | (17) |
式中fD表示多普勒频率。
3 数值结果及讨论讨论宏蜂窝M2M信道模型中的传输特性,模拟分析采用变量:f=5.9 GHz, K=10, vT=10 m/s, vR=20 m/s, yT=π/3, yR=π/3。
图 2为空间互相关函数ρhpq, hp′q′(t, τ)在不同传播时延τ和不同运动时间t的分析结果。传播时延值τ上升,空间相关性下降缓慢,通过增加运动时间t可以看到类似现象。分析结果和文献[14]一致,验证了分析的准确性。
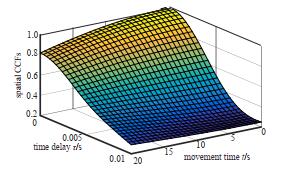 |
| Fig.2 Spatial CCFs of the proposed model for different propagation delay τ and different movement time instant t 图 2 模型对不同传播延迟τ和不同运动时间瞬时t空间互相关函数 |
图 3为空间互相关函数ρhpq, hp′q′(t, τ)对不同的天线间距бT和бR的分析结果。可以看到,当发射和接收天线间距增加时,空间相关性逐渐降低,这与文献的测量结果相符合。
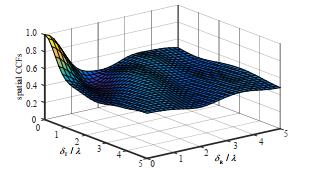 |
| Fig.3 Analytical results of the spatial CCFs of the proposed model for different antenna spacings of the Tx and Rx 图 3 Tx和Rx不同天线间距模型的空间互相关函数的分析结果 |
图 4为两种非视距传播路径在不同时间间隔和位移的空间互相关函数。由图 4可以观察到,当运动时间t从0 s增加到10 s时,由于Tx和Rx运动引起的角变量变化,空间相关性逐渐增加。与上述模拟和分析结果相比,发现提出的信道模型运算结果更好,验证了模拟结果的正确性。
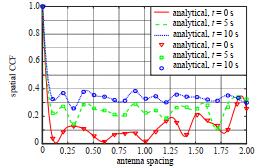 |
| Fig.4 Analysis and simulation results of spatial cross-correlation function at different time instants t 图 4 不同时间瞬间t下的空间互相关函数的分析和模拟 |
把p=p′, q=q′和бT=бR=0代入式(16)。图 5为提出的模型时间自相关函数ρhpq(t, Δt)的非视距分量在不同运动时间t的分析和仿真结果。值得注意的是,运动时间t的变化范围从0 s到10 s,伴随着多普勒频率的变化, 时间自相关函数呈现不同的仿真结果。此外,分析结果与模拟结果在不同时间点的时间相关性是一致的,证实了上述分析的正确性。
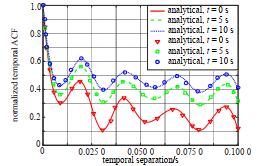 |
| Fig.5 Analysis and simulation results of time autocorre lation function at different time instants t 图 5 5不同时间瞬间t下的时间自相关函数的分析和模拟 |
图 6为信道模型时间自相关函数ρhpq(t, Δt)在Tx和Rx不同运动方向的分析结果。当运动方向从Tx到Rx,γT=0到γT=π以及γR=0到γR=0相应增加,这种情况下,有效散射体所反映的各分量的时间相关性降低缓慢。
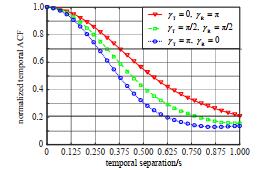 |
| Fig.6 Analysis and simulation results of time autocorrelation functions of Tx and Rx in different directions of movement 图 6 Tx和Rx在不同运动方向的时间自相关函数的分析和模拟 |
根据文献[16],分析和模拟了不同运动时间瞬时t的多普勒功率谱密度Shpq(fD, t),分析和仿真结果如图 7,多普勒频谱的分布曲线随时间逐渐减少。此外,多普勒频谱的分析结果与仿真结果很好地吻合,进一步验证了宏蜂窝M2M信道多普勒频谱推导的准确性。
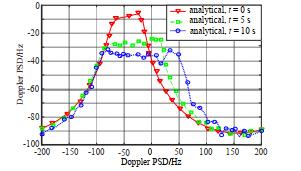 |
| Fig.7 Analytical and simulation results of the Doppler PSDs for different movement time instants t 图 7 不同运动时间瞬时t的多普勒功率谱密度的分析和模拟 |
本文提出一个5G宏蜂窝移动通信三维圆柱MIMO信道模型。该模型推导了视距传播分量的空间互相关函数(CCFs)、时间自相关函数(ACFs)和多普勒功率谱密度(PSDs)的闭合表达式,以及受干扰物体非视距(NLoS)反射分量的闭式表达式。结果表明,随着运动时间的变化,该模型的CCFs呈现出不同的分布曲线。随着传播延迟或运动时间的增大,CCFs的值逐渐减小;Tx和Rx的运动引起多普勒功率谱密度(PSDs)分布曲线随运动时间的增加逐渐下降。模型的传输特性分析与仿真果吻合较好,可应用于5G宏蜂窝移动通信系统的评估和设计。
| [1] |
SUN X, GUI G, LI Y, et al. ResInNet:a novel deep neural network with feature re-use for internet of things[J]. IEEE Internet of Things Journal, 2019, 6(1): 679-691. |
| [2] |
SUN J, SHI W, YANG Z, et al. Behavioral modeling and linearization of wideband RF power amplifiers using BiLSTM networks for 5G wireless systems[J]. IEEE Transactions on Vehicular Technology, 2019, 68(11): 10348-10356. DOI:10.1109/TVT.2019.2925562 |
| [3] |
JIANG H, ZHANG Z, DANG J, et al. A novel 3D massive MIMO channel model for vehicle-to-vehicle communication environments[J]. IEEE Transactions on Communications, 2018, 66(1): 79-90. DOI:10.1109/TCOMM.2017.2751555 |
| [4] |
JIANG H, ZHANG Z, DANG J, et al. Analysis of geometric multibounced virtual scattering channel model for dense urban street environments[J]. IEEE Transactions on Vehicular Technology, 2017, 66(3): 1903-1912. DOI:10.1109/TVT.2016.2574925 |
| [5] |
BEAULIEU N C, XIE J. A novel fading model for channels with multiple dominant specular components[J]. IEEE Wireless Communications Letters, 2015, 4(1): 54-57. |
| [6] |
BI Y, ZHANG J, ZHU Q, et al. A novel non-stationary High-Speed Train (HST) channel modeling and simulation method[J]. IEEE Transactions on Vehicular Technology, 2019, 68(1): 82-92. |
| [7] |
WU S, WANG C X, AGGOUNE E H M, et al. A general 3-D non-stationary 5G wireless channel model[J]. IEEE Transactions on Communications, 2018, 66(7): 3065-3078. DOI:10.1109/TCOMM.2017.2779128 |
| [8] |
CHENG X, WANG C X, LAURENSON D I, et al. An adaptive geometry-based stochastic model for non-isotropic MIMO mobile-to-mobile channels[J]. IEEE Transactions on Wireless Communications, 2009, 8(9): 4824-4835. DOI:10.1109/TWC.2009.081560 |
| [9] |
PETRUS P, REED J H, RAPPAPORT T S. Geometrical-based statistical macrocell channel model for mobile environments[J]. IEEE Transactions on Communications, 2002, 50(3): 495-502. DOI:10.1109/26.990911 |
| [10] |
HE R, AI B, STUBER G L, et al. Mobility model based non-stationary mobile-to-mobile channel modeling[J]. IEEE Transactions on Wireless Communications, 2018, 17(99): 4388-4400. |
| [11] |
ZHANG J, PAN C, PEI F, et al. Three-dimensional fading channel models:a survey of elevation angle research[J]. IEEE Communications Magazine, 2014, 52(6): 218-226. DOI:10.1109/MCOM.2014.6829967 |
| [12] |
YU Y, ZHANG J, SMITH P J, et al. Theoretical analysis of 3-D channel spatial correlation and capacity[J]. IEEE Communications Letters, 2018, 22(2): 420-423. DOI:10.1109/LCOMM.2017.2765307 |
| [13] |
JIANG H, ZHANG Z, WU L, et al. A 3-D non-stationary wideband geometry-based channel model for MIMO vehicle-to-vehicle communications in tunnel environments[J]. IEEE Transactions on Vehicular Technology, 2019, 68(7): 6257-6271. DOI:10.1109/TVT.2019.2918333 |
| [14] |
YUAN Yi, WANG Chengxiang, HE Yejun, et al. 3D wideband non-stationary geometry-based stochastic models for non-isotropic MIMO vehicle-to-vehicle channels[J]. IEEE Transactions on Wireless Communications, 2015, 14(12): 6883-6895. DOI:10.1109/TWC.2015.2461679 |
| [15] |
NAWAZ S J, QURESHI B H, KHAN N M. A generalized 3-D scattering model for a macrocell environment with a directional antenna at the BS[J]. IEEE Transactions on Vehicular Technology, 2010, 59(7): 3193-3204. DOI:10.1109/TVT.2010.2050015 |
| [16] |
ZHOU J, JIANG H, KIKUCHI H. Generalised three-dimensional scattering channel model and its effects on compact multiple-input and multiple-output antenna receiving systems[J]. IET Communications, 2015, 9(18): 2177-2187. DOI:10.1049/iet-com.2014.1059 |
| [17] |
ZAJIC A G. Impact of moving scatterers on vehicle-to-vehicle narrow-band channel characteristics[J]. IEEE Transactions on Vehicular Technology, 2014, 63(7): 3094-3106. DOI:10.1109/TVT.2014.2299239 |
| [18] |
JIANG H, ZHANG Z, GUI G. Three-dimensional non-stationary wideband geometry-based UAV channel model for A2G communication environments[J]. IEEE Access, 2019(7): 26116-26122. |
| [19] |
CHANG H, BIAN J, WANG C, et al. A 3D non-stationary wideband GBSM for low-altitude UAV-to-ground Ⅴ2Ⅴ MIMO channels[J]. IEEE Access, 2019(7): 70719-70732. |
| [20] |
KAREDAL J, TUFVESSON F, CZINK N, et al. A geometry-based stochastic MIMO model for vehicle-to-vehicle communications[J]. IEEE Transactions on Wireless Communications, 2009, 8(7): 3646-3657. DOI:10.1109/TWC.2009.080753 |
| [21] |
HE R, MOLISCH A F, TUFVESSON F, et al. Vehicle-to-vehicle propagation models with large vehicle obstructions[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(5): 2237-2248. DOI:10.1109/TITS.2014.2311514 |
| [22] |
BI Y, ZHANG J, ZHU Q, et al. A novel non-stationary High-Speed Train (HST) channel modeling and simulation method[J]. IEEE Transactions on Vehicular Technology, 2019, 68(1): 82-92. |
| [23] |
HUANG H, SONG Y, YANG J, et al. Deep-learning-based millimeter-wave massive MIMO for hybrid precoding[J]. IEEE Transactions on Vehicular Technology, 2019, 68(3): 3027-3032. DOI:10.1109/TVT.2019.2893928 |
| [24] |
HUANG H, YANG J, SONG Y, et al. Deep learning for super-resolution channel estimation and DOA estimation based massive MIMO system[J]. IEEE Transactions on Vehicular Technology, 2018, 67(9): 8549-8560. DOI:10.1109/TVT.2018.2851783 |
| [25] |
JIANG H, ZHANG Z, GUI G. A novel estimated wideband geometry-based vehicle-to-vehicle channel model using an AOD and AOA estimation algorithm[J]. IEEE Access, 2019(7): 35124-35131. |
| [26] |
ABDI A, BARGER J A, KAVEH M. A parametric model for the distribution of the angle of arrival and the associated correlation function and power spectrum at the mobile station[J]. IEEE Transactions on Vehicular Technology, 2002, 51(3): 425-434. DOI:10.1109/TVT.2002.1002493 |
 2020, Vol. 18
2020, Vol. 18


