2. 贵州大学 公共大数据国家重点实验室,贵州 贵阳 550025
2. State Key Laboratory of Public Big Data, Guizhou University, Guiyang Guizhou 550025, China
20世纪60年代,自适应波束形成与波达方位估计共同构建了阵列信号处理的重要内容。经过多年的发展,自适应波束形成技术已广泛用于无线通信、雷达、医学成像、射电天文等领域。传统波束形成能够使期望信号来波方向上形成良好的主波束,具有很优秀的空间分辨能力以及减弱干扰的功能。但其先决条件是建立在基阵对感兴趣信号响应准确已知的基础上。但实际应用环境存在诸多如阵列通道不一致性(幅相误差)、阵列位置的扰动、小快拍、干扰信号与期望信号相干等非理想因素,使得波束形成方法输出性能受到严重影响。相对于传统波束形成,Capon波束形成方法利用采样协方差矩阵取代干扰加噪声协方差矩阵,性能有一定提升,但在高信噪比情况下和小快拍数下,并不能最大发挥波束形成的功能。在现代空中作战中,非协同接收条件下,得到的数据信息量很少,即小快拍,如战斗机高速运动的情况下。由于时间短,只能得到较少的稳态数据,对数据协方差矩阵的估计产生较大的偏差。波束形成中,一旦快拍数小于某一值时,输出信干噪比会急剧下降,尤其是采样协方差矩阵中包含较强期望信号分量的情况。另外,在很多常规的波束形成方法中,通常假设干扰与干扰之间以及与期望信号之间是不相关的、相互独立的,才能得到令人满意的性能输出。实际应用中,干扰环境却是复杂多变的,模拟和目标信号常常是相干的,如存在干扰器、声诱饵、模拟器等,以诱导战斗机。为提高波束形成方法的鲁棒性,研究者设计了大量的鲁棒自适应波束形成器。文献[1]提出一种基于协方差矩阵重建的稳健波束形成方法,具有良好的抗强期望信号背景的能力。但在低信噪比情况下,在干扰信号方向不再置零,甚至变成非自适应的方法,效果如同对角加载方法中加载因子过大一样。文献[2-4]也提出一些基于协方差矩阵重构的波束形成方法。但这些算法首先必须通过低分辨力DOA估计出感兴趣信号的波达角,然后采用Capon空间谱重建干扰加噪声协方差矩阵,这相当于使用了2种算法。且Capon空间谱的准确性在相干干扰存在时,对功率的预估会有严重的偏差,不再适用相干干扰存在的情况。对此,文献[5]提出一种基于迭代自适应方法的干扰加噪声协方差矩阵重建方法。该方法可以处理相干信号,同时对于阵列扰动和有限采样效应具有稳健性。但构建出的协方差矩阵并不精确。文献[6]在嵌套阵列背景下提出稀疏表示方法估计信号功率,重构干扰加噪声功率提升波束形成的性能,但采用凸优化方法使计算量大大增加,不利于实时实现。
本文提出了基于迭代自适应法(IAA)的协方差矩阵重构稳健波束形成方法。该方法利用IAA估计出精确的方位角和功率谱[7-8],IAA不依赖于信号的非相干假设,解决了相干信号存在下的方位估计和功率估计;进一步利用估计的功率重构干扰协方差矩阵,在重构中,将积分区域缩小到三维立体环域,减少无用信息的影响,提高了干扰协方差矩阵的重构精确度,最终通过波束形成来抑制干扰信号。
1 问题描述假设有Q+1个相互独立窄带信号入射到M元均匀线列阵,其中M > Q+1,入射信号s(t)与噪声v(t)相互独立,则阵列接收信号可表示为:
| $ {x}(t) = {As}(t) + {\upsilon} (t) $ | (1) |
式中
| $ \left\{ \begin{array}{l} \min \;\;{{\omega} ^H}{{R}_{i + n}}{\omega} \\ {\rm s.t} \quad {{\omega} ^H}{a}({\theta _0}) = 1 \end{array} \right. $ | (2) |
其最优解为:
| $ {{\omega} _{opt}} = \frac{{{R}_{i + n}^{ - 1}{a}({\theta _0})}}{{{{a}^H}({\theta _0}){R}_{i + n}^{ - 1}{a}({\theta _0})}} $ | (3) |
式中Ri+n为干扰加噪声协方差矩阵。实际中由于快拍数的采样数目有限,协方差矩阵Ri+n不能直接得到,常用采样协方差矩阵Rxx代替Ri+n。此时,Capon波束形成的权矢量可表示为:
| $ {{\mathit{\boldsymbol{ \pmb{\mathsf{ ω}}} }}_{capon}} = \frac{{{\mathit{\boldsymbol{\hat R}}}_{xx}^{ - 1}{\mathit{\boldsymbol{\bar a}}}({\theta _0})}}{{{{{\mathit{\boldsymbol{\bar a}}}}^H}({\theta _0}){\mathit{\boldsymbol{\hat R}}}_{xx}^{ - 1}{\mathit{\boldsymbol{\bar a}}}({\theta _0})}} $ | (4) |
式中a(θ0)为估计的期望信号导向矢量。由式(4)可知,若期望信号的功率很强,波束形成器会抑制期望信号,即高信噪比性能会下降。除此之外,Capon波束形成只能用于干扰和信号互不相关的情况。为提升波束形成方法在这些不利条件下的干扰抑制性能,本文提出基于IAA的协方差矩阵重构稳健波束形成方法。此方法以迭代自适应思想高分辨估计信号与干扰的功率和方位,采用三维立体积分重构干扰协方差矩阵,进而计算出波束形成权系数。该方法不受相干源的影响,降低了不精确噪声加干扰对干扰抑制的影响。
2 迭代自适应法迭代自适应空间谱估计方法是一种基于加权最小二乘的非参数化谱估计方法。其主要思想是把潜在的来波方向(-90°~90°)以足够小的角度划分为K(K>>M)个网格点,假设感兴趣的信号来波方向包含在离散化的各个网格角度中,估计第k个方向上的空间功率谱
对于阵列观测数据模型
| $ {x}(n) = {As}(n) + {\upsilon} (n) $ | (5) |
式中
| $ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\hat P_k} = \frac{1}{N}\sum\limits_{n = 1}^N {{{\left| {{{\hat s}_k}(n)} \right|}^2}} , {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k = 1, 2, \cdots , K $ | (6) |
IAA通过求解如下加权最小二乘优化问题:
| $ \mathop {\min }\limits_{{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \theta } }_k}, {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over s} }_k}} \sum\limits_{t = 1}^T {{{\left[ {{x}(t) - {a}({{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \theta } }_k}){{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over {s}} }_k}(t)} \right]}^H}{W}\left[ {{x}(t) - {a}({{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \theta } }_k}){{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over {s}} }_k}(t)} \right]} $ | (7) |
式中W为正定、共轭对称加权矩阵。若R为阵列信号协方差矩阵,Q(θk)为θk以外其他方向上所有干扰和噪声的协方差矩阵。有
| $ {Q}({\theta _k}) = {R} - {a}({\theta _k}){{a}^H}({\theta _k}){P_k} $ | (8) |
式中
| $ {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over s} _k}(t) = \frac{{{{a}^H}({\theta _k}){{R}^{ - 1}}{x}(t)}}{{{{a}^H}({\theta _k}){{R}^{ - 1}}{a}({\theta _k})}} $ | (9) |
IAA采用最小二乘法估计初值
IAA没有对信号的相关性做任何假设,直接根据式(6)构造空间功率谱对角阵P,所以可处理相干信号源,能够精准估计任何类型信号的方位。
3 基于IAA的协方差矩阵重构稳健波束形成方法经典Capon波束形成方法,采用样本协方差代替干扰加噪声协方差,抑制干扰性能不佳。文献[2]中的协方差矩阵方法改善了干扰加噪声协方差的重构性能,但是通过扇面积分重构干扰协方差,必然引入不必要的成分。本文首先利用IAA估计精确的干扰功率
| $ {{\mathit{\boldsymbol{\hat R}}}_{{\mathop{\rm int}} }} = \frac{1}{2}\int_{\partial {S_a}(\theta \in {\Phi _{{\mathop{\rm int}} }})} {{{\hat P}_{Capon}}{a}{{a}^H}} d\theta $ | (10) |
式中
| $ {{{\mathit{\boldsymbol{\hat R}}}}_{{\mathop{\rm int}} }} = \frac{1}{2}\int_{\partial {S_a}(\theta \in {\Phi _{{\mathop{\rm int}} }})} {{{\hat P}_k}{a}{{a}^H}d\theta } $ | (11) |
式中干扰功率
对于噪声协方差矩阵,可以通过
| $ {{\mathit{\boldsymbol{\hat R}}}_{{\rm i} + {\rm n}}} = { {\mathit{\boldsymbol{\hat R}}}_{{\mathop{\rm int}} }} + \hat \sigma _n^2{I} $ | (12) |
最终得到IAA-SpaCov方法最优权矢量的表达式为:
| $ {{\omega} _{{\rm{IAA - SpaCov}}}} = \frac{{ {\mathit{\boldsymbol{\hat R}}}_{{\rm i} + {\rm n}}^{ - 1}{a}({\theta _0})}}{{{{a}^H}({\theta _0}) {\mathit{\boldsymbol{\hat R}}}_{{\rm i} + {\rm n}}^{ - 1}{a}({\theta _0})}} $ | (13) |
仿真中采用M=10个全向传感器组成的均匀线阵列,阵列间距为半个波长。噪声建模为零均值的高斯分布白噪声。假定2个干扰源来波方向角度分别为θ1=-40°和θ2=60°,且有一干扰信号与期望信号相干,干扰噪声比(INR)等于20 dB;期望信号为来自θ0=0°的平面波。假定相位误差和阵元位置误差同时存在,相位误差为[0.025π, 0]的正态分布,阵元位置误差为[0.05, 0.1]的正态分布。
在不同SNR、不同快拍数下,分别在存在相位和阵元位置误差时,对RCB[10], REC[2], IAA-SectorCov方法[5]和IAA-SpaCov进行仿真对比。
在IAA-SectorCov方法中,θ取值为[-5, 5],K=180,整个空间范围为-90°~90°。在方法IAA-SpaCov中,基于高维环重构协方差矩阵部分参数的设置为:假设期望信号和干扰的角扇区分别为
| $ {{{a}}_{il}}={\mathit{\boldsymbol{\bar{a}}}}({{\theta }_{i}})+{\zeta }/{\sqrt{M}\left[ {{\rm e}^{{\rm j}\varphi _{0}^{l}}},{{\rm e}^{{\rm j}\varphi _{1}^{l}}},\cdots ,{{\rm e}^{{\rm j}\varphi _{M-1}^{l}}} \right]}\; $ | (14) |
式中
仿真1:不同快拍数下的Capon与IAA谱估计比较
当SNR分别为20 dB时,快拍数分别设定为100, 500次,比较Capon与IAA谱估计的性能。
由图 1可知,对于相干信号,当快拍数较大时,Capon结果很不理想,但IAA谱估计结果很理想,基本不受相干的影响。当快拍数较小时,Capon谱估计已经失效,对角度和功率谱的估计已不再准确,但IAA方法依然没有受到影响,有很好的估计性能。由上面的仿真可知,IAA方法在小快拍和相干干扰存在的情况下不仅具有很好的角度估计,且能够比较精确地估计该方位上的功率谱。因此本文采用IAA估计功率谱来重构干扰协方差矩阵,会取得更好的干扰抑制效果。
 |
| Fig.1 Spatial spectrum versus number of snapshots 图 1 不同快拍数下的空间谱估计 |
仿真2:不同信噪比下的波束图
当存在相位误差和阵元位置误差时,将快拍数固定为1 000次,图 2(a)~(b)分别比较了SNR为0 dB, 20 dB的情况下,RCB, REB, IAA-SectorCov和IAA-SpaCov的归一化波束图。
 |
| Fig.2 Beam pattern of the beamformers versus SNR 图 2 不同SNR下的归一化波束图 |
图 2(a)~(b)中可以看出,当存在相位误差和阵元位置误差时,无论信噪比的大小,IAA-SpaCov主波束能够准确地对准期望信号的方向,并且在干扰方向生成零陷。IAA-SpaCov比IAA-SectorCov缩小了积分区域,减少无用信息,因此旁瓣比IAA-SectorCov更低,性能更优。
仿真3:不同输入SNR下的输出SINR
当存在相位误差和阵元位置误差时,将快拍数固定为1 000次。信噪比在-10~20 dB变化,每个信噪比执行100次Monte-Carlo实验。图 3为RCB, REB, IAA-SectorCov和IAA-SpaCov在不同SNR下输出SINR的关系曲线。可以看出,当存在相位误差和阵元位置误差时,相较于RCB随信噪比的增加,IAA-SpaCov, IAA-SectorCov, REB方法都显示出优良的SINR性能。尤其是随着SNR的增加,IAA-SpaCov逐渐接近最优SINR。原因是IAA-SpaCov将积分区域以平面区域缩小到三维环域区域,提高了协方差重构精确度,输出结果最接近最优输出SINR。
 |
| Fig.3 Output SINR versus SNR 图 3 不同SNR下的输出SINR |
仿真4:随快拍数变化的SINR
当存在相位误差和阵元位置误差时,RSN=10 dB,每一个快拍执行100次Monte-Carlo实验。图 4为RCB, REB, IAA-SectorCov和IAA-SpaCov输出SINR随快拍数的变化曲线。
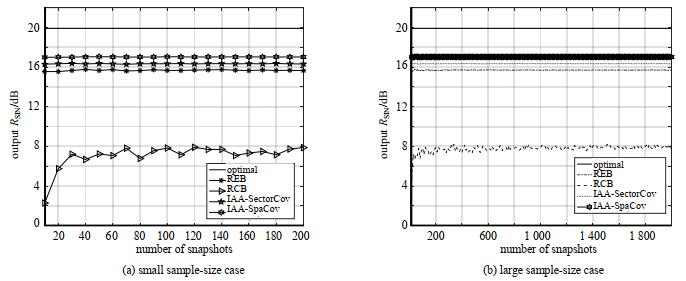 |
| Fig.4 Output SINR versus the number of snapshots 图 4 不同快拍数下的输出SINR |
图 4(a)为小快拍情况下的输出SINR与样本数的关系。可以看出,当存在相位误差和阵元位置误差时,提出IAA-SpaCov, IAA-SectorCov, REB方法在小快拍数条件下,都能很快达到收敛值,且提出方法在输出性能上仍具有明显的优势。图 4(b)为多快拍情况下的输出SINR与样本数的关系。当所有方法达到稳健值时,IAA-SpaCov在这些方法中输出效果最好。原因主要是IAA-SpaCov一方面通过IAA方法得到了精确的功率谱估计,另一方面,环域三维立体积分减少了无用信息的影响。
5 结论为提升在相干信号及小样本背景下的干扰抑制性能,提出了一种基于IAA功率谱积分的协方差矩阵重构稳健波束形成方法。该方法通过IAA求得精准的功率谱,进而将积分区域缩小到三维立体环,减少无用信息的影响,精确重构干扰协方差矩阵。IAA能够在干扰相干的情况下精确得到方位信息,避免了导向矢量估计不准带来的影响。通过三维立体积分精确得到干扰的协方差矩阵,提高了波束形成的性能。仿真实验表明,该方法在相干信号、少快拍、相位及阵元位置误差同时存在的情况下,能够抑制掉干扰信号,输出SINR非常接近最优输出SINR。
| [1] |
MU P C, LI D, YIN Q, et al. Robust MVDR beamforming based on covariance matrix reconstruction[J]. Science China(Information Sciences), 2013, 56(4): 1-12. |
| [2] |
GU Y, LESHEM A. Robust adaptive beamforming based on interference covariance matrix reconstruction and steering vector estimation[J]. IEEE Transactions on Signal Processing, 2012, 60(7): 3881-3885. DOI:10.1109/TSP.2012.2194289 |
| [3] |
GONG C, HUANG L, XU D, et al. Knowledge-aided robust adaptive beamforming with small snapshots[J]. Electronics Letters, 2013, 49(20): 1259-1261. DOI:10.1049/el.2013.2447 |
| [4] |
HUANG L, ZHANG J, XU X, et al. Robust adaptive beamforming with a novel interference-plus-noise covariance matrix reconstruction method[J]. IEEE Transactions on Signal Processing, 2015, 63(7): 1643-1650. DOI:10.1109/TSP.2015.2396002 |
| [5] |
WANG Y, BAO Q, CHEN Z. Robust adaptive beamforming using IAA-based interference-plus-noise covariance matrix reconstruction[J]. Electronics Letters, 2016, 52(13): 1185-1186. DOI:10.1049/el.2015.4420 |
| [6] |
周荣艳, 李孟, 谭伟杰. 基于嵌套阵列的稀疏表示稳健波束形成方法[J]. 太赫兹科学与电子信息学报, 2019, 17(3): 462-468. (ZHOU Rongyan, LI Meng, TAN Weijie. Sparsity-based robust beamforming method using nested array[J]. Journal of Terahertz Science and Electronic Information Technology, 2019, 17(3): 462-468.) |
| [7] |
DU L, YARDIBI T, LI J, et al. Review of user parameter-free robust adaptive beamforming algorithms[J]. Digital Signal Processing, 2009, 19(4): 567-582. DOI:10.1016/j.dsp.2009.02.001 |
| [8] |
BARCELO M, LOPEZ-VICARIO J, SECO-GRANADOS G. A reduced complexity approach to IAA beamforming for efficient DOA estimation of coherent sources[J]. EURASIP Journal on Advances in Signal Processing, 2011(1): 521265. |
| [9] |
鲁欢, 冯西安. 联合协方差矩阵重构与导向矢量校正的稳健波束形成方法[J]. 探测与控制学报, 2018, 40(1): 21-26, 32. (LU Huan, FENG Xi'an. Joint interferenceplus-noise covariance matrix reconstruction with steering vector calibration for robust beamforming[J]. Journal of Detection & Control, 2018, 40(1): 21-26, 32.) |
| [10] |
LI J, STOICA P, WANG Z. On robust Capon beamforming and diagonal loading[J]. IEEE Transactions on Signal Processing, 2007, 51(7): 1702-1715. DOI:10.3724/SP.J.1146.2011.00127 |
 2020, Vol. 18
2020, Vol. 18

