快速傅里叶变换(FFT)算法具有计算量小的显著优点,在信号处理技术领域得到了广泛应用,现已成为数字信号处理强有力的工具。FFT硬件实现速度取决于算法效率,目前基于现场可编程逻辑门阵列(FPGA)平台实现的FFT算法IP核大多采用库利-图基基-2、基-4或者二者混合算法,要求其变换长度
有限列长为N的序列
| $X(k) = \sum\limits_{n = 0}^{N - 1} {x(n){{\rm{e}}^{ - {\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}}}{N}nk}}} = \sum\limits_{n = 0}^{N - 1} { x(n)W_N^{nk}, W_N^{}} = {{\rm{e}}^{ - {\rm{j}}\frac{{2{\rm{ \mathsf{ π} }}}}{N}}}, k = 0, 1, \cdots , N - 1$ | (1) |
式中
| $\left\{ \begin{array}{l} n = f({n_1}, {n_2}) = ({N_2}{n_1} + {A_2}{n_2})\bmod N, {n_1}, {k_1} = 0, 1, \cdots , {N_1} - 1{\kern 1pt} , {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} N = {N_1}{N_2} \\ k = \overline f ({k_1}, {k_2}) = ({B_1}{k_1} + {N_1}{k_2})\bmod N, {n_2}, {k_2} = 0, 1, \cdots , {N_2} - 1 \\ \end{array} \right.$ | (2) |
函数
素因子算法(Prime Factor Algorithm,PFA)采用点数互素的短点数DFT运算的组合来完成长点数的运算。这种实现方法不会引入额外的与旋转因子相乘的运算,因而该方法的乘法运算次数相对于库利-图基算法要少得多。素因子算法的特点是既能减少乘法运算次数,还有便于程序实现的结构。在通用机上,它的效率是最高的。不过,该算法是以更加复杂的下标变换为代价来消除旋转因子。将FFT序列分为互质的小序列,可先分别计算小序列变换,再得到N点变换。N1和N2互质,且合理选择A2和B1的值,使其满足[7]:
| $ < {N_2}{B_1}{ > _N} = {N_2}, < {A_2}{N_1}{ > _N} = {N_1}, < {A_2}{B_1}{ > _N} = 0$ | (3) |
式中
| ${A_2} = {p_1}{N_1} = {q_1}{N_2} + 1{\kern 1pt} , {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {B_1} = {p_2}{N_2} = {q_2}{N_1} + 1$ | (4) |
此时A2, B1, p1, q1, p2, q2均为正整数,则可将DFT进行如下分解:
| $X(k) = X({k_1}, {k_2}){\rm{ = }}\sum\limits_{{n_2}} {\sum\limits_{{n_1}} {x({n_1}, {n_2})W_N^{({N_2}{n_1} + {A_2}{n_2})({B_1}{k_1} + {N_1}{k_2})}} } {\rm{ = }}\sum\limits_{{n_2}} {\sum\limits_{{n_1}} {x({n_1}, {n_2})W_{{N_1}}^{{n_1}{k_1}}} } W_{{N_2}}^{{n_2}{k_2}} = \sum\limits_{{n_2}} {\left[ {\sum\limits_{n1} {x({n_1}, {n_2})W_{{N_1}}^{{n_1}{k_1}}} } \right]W_{{N_2}}^{{n_2}{k_2}}} {\rm{ = }}\sum\limits_{{n_2}} {{X_1}({k_1}, {n_2})} W_{{N_2}}^{{n_2}{k_2}}$ | (5) |
库利-图基算法(Cooly-Tukey Algorithm,CTA)1965年由J W库利和T W图基提出,是最常见的快速傅里叶变换算法。采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少,特别是被变换的抽样点数N越多,FFT算法计算量的节省就越显著。该算法成功地将计算离散傅里叶变换的时间复杂度从
| $X(k) = X({k_1}, {k_2}){\rm{ = }}\sum\limits_{n2} {\sum\limits_{{n_1}} {x({n_1}, {n_2})W_{{N_1}}^{{n_1}{k_1}}} } W_{{N_2}}^{{n_2}{k_2}}W_N^{{n_2}{k_1}} = \sum\limits_{{n_2}} {\left\{ {W_N^{{n_2}k_1^{}}\left[ {\sum\limits_{{n_1}} {x({n_1}, {n_2})W_{{N_1}}^{{n_1}{k_1}}} } \right]} \right\}} W_{{N_2}}^{{n_2}{k_2}}{\rm{ = }}\sum\limits_{{n_2}} {\left[ {W_N^{{n_2}k_1^{}}{X_1}({k_1}, {n_2})} \right]} W_{{N_2}}^{{n_2}{k_2}}$ | (6) |
通过与式(2)中的映射关系进行观察对比,如果用数位形式表示对n和k的分解,可以得到如下表达形式:
| $n = f({n_1}, {n_2}) = {({n_1}, {n_2})_{{\rm{digit}}}}{\kern 1pt} {\kern 1pt} , {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k = \overline f ({k_1}, {k_2}) = {({k_2}, {k_1})_{{\rm{digit, reverse}}}}$ | (7) |
式中:n和k的数位表示是颠倒的,同时颠倒的还有各个数位的基。因此,当需要顺序输入同时保证顺序输出时,在I/O的过程中应当进行适当的操作,其他中间步骤不会受到影响。这个性质是PFA所不具备的。尽管在由分解得到一维表示时都是简单的加权求和(PFA需要额外的取模运算),但在逆运算时则存在很大的差别。由于CTA数位表示的顺序性,它的逆运算可以通过多级计数器实现,而该过程对于PFA非常复杂。
2 新型混合基算法设计与实现通过将PFA算法的分解公式(5)与CTA算法的分解公式(6)进行对比可以发现,CTA较之PFA中间多了一级旋转因子的乘法,而对于索引的计算,PFA会比CTA复杂很多。对于一个已经给定长度为N的FFT,设计的FFT算法是PFA与CTA的结合,从而使各自的优点能够充分发挥。具体而言,先利用PFA将N分解为两个互素的因子N1和N2,
对N1分解是为了更高效计算:
| ${X_1}({k_1}, {n_2}) = \sum\limits_{{n_1}} {x({n_1}, {n_2})W_{{N_1}}^{{n_1}{k_1}}} $ | (8) |
上式可进一步分解为:
| $\left\{ \begin{array}{l} {n_1} = ({n_{1, 1}}, \widetilde {{n_{1, 2}}}) = ({n_{1, 1}}, {n_{1, 2}}, \cdots , {n_{1, r}}, \widetilde {{n_{1, r + 1}}}) = ({n_{1, 1}}, {n_{1, 2}}, \cdots , {n_{1, {R_1}}}) \\ {k_1} = ({k_{1, 1}}, \widetilde {{k_{1, 2}}}) = ({k_{1, 1}}, {k_{1, 2}}, \cdots , {k_{1, r}}, \widetilde {{k_{1, r + 1}}}) = ({k_{1, 1}}, {k_{1, 2}}, \cdots , {k_{1, {R_1}}}) \\ \end{array} \right.$ | (9) |
其中,
| $\left\{ \begin{array}{l} \widetilde {{n_{1, r}}}, \widetilde {{k_{1, r}}} = 0, 1, \cdots , \widetilde {{N_{1, r}}} - 1; {n_{1, r}}, {k_{1, r}} = 0, 1, \cdots , {N_{1, r}} - 1 \\ \widetilde {{n_{1, r}}} = ({n_{1, r}}, \widetilde {{n_{1, r + 1}}}) = ({n_{1, r}}, {n_{1, r + 1}}, \cdots , {n_{1, {R_1}}}); \widetilde {{N_{1, r}}}{\rm{ = }}{N_{1, r}}\widetilde {{N_{1, r + 1}}} = {N_{1, r}}{N_{1, r + 1}}\; \cdots {N_{1, {R_1}}} \\ \end{array} \right.$ | (10) |
可得到类似文献[8]中的递推公式:
| ${X_{1, r}}({k_{1, 1}}, {k_{1, 2}}, \cdots , {k_{1, r}}, \widetilde {{n_{1, r + 1}}}, {n_2}) = \left[ {\sum\nolimits_{{n_{1, r}}} {{X_{1, r - 1}}} ({k_{1, 1}}, {k_{1, 2}}, \ldots , {n_{1, r}}, \widetilde {{n_{1, r + 1}}}, {n_2})W_{{N_{1, r}}}^{{n_{1, r}}{k_{1, r}}}} \right]W_{\widetilde {{N_{1, r}}}}^{\widetilde {{n_{1, r + 1}}}{k_{1, r}}}$ | (11) |
式(11)中这个迭代过程一共有R1步,称
| ${X_{1, r}}({k_{1, 1}}, {k_{1, 2}}, \cdots , {k_{1, r}}, {n_{1, r + 1}}, {n_{1, {R_1}}}, {n_2}) = {X_{1, r - 1}}({k_{1, 1}}, {k_{1, 2}}, \cdots , {n_{1, r}}, {n_{1, r + 1}}, {n_{1, {R_1}}}, {n_2})W_{{N_{1, r}}}^{{n_{1, r}}{k_{1, r}}}$ | (12) |
其中输入和输出的索引值的区别仅在于第r维,即将
而旋转因子可变换为:
| $W_{\widetilde {{N_{1, r}}}}^{\widetilde {{n_{1, r + 1}}}{k_{1, r}}} = W_{N1}^{{N_{1, 1}} \cdots {N_{1, r - 1}}({n_{1, r + 1}} \cdots {n_{1, {R_1}}}){k_{1, r}}}$ | (13) |
因此,若查找表中保存有
由于算法采用的是顺序存储结构,关键在于将多维分解表示转化为一维形式,即将
| $n = ({N_2}{n_1} + ({q_1}{N_2} + 1){n_2})\,\bmod \,N = ({N_2}({n_1} + {q_1}{N_2}) + {n_2})\,\bmod \,N = {N_2}{n'_1} + {n_2}$ | (14) |
式中
本算法中,蝶形运算采用高效的维诺格兰傅里叶变换算法(Winograd Fourier Transform Algorithm,WFTA)。如果不同的基采用不同的蝶形单元,则蝶形单元模块将会占用一部分存储资源,因此也需要一种蝶形单元模块能够同时适用于基-2、基-3、基-4。在一个蝶形运算模块内部包含所有3种基的蝶形运算[10]。
将蝶形运算模块分为3个独立的流水线步骤,每个步骤使用一个DSP slice,分别对应pre-add、multiply以及post-add三个操作,基-2、基-3和基-4都可以映射到这样的硬件结构,从而降低复杂度并减少资源消耗。以基-3算法为例,蝶形运算的分解如图 1所示,其中控制信号C0及其乘因子值的配置情况由表 1给出。对N2的分解与N1类似,区别在于此时固定的是k1而不是n2,对N2进行与N1类似的操作后即可完成高效计算。该混合基FFT算法基于基-2、基-3、基-4进行混合基FFT运算,也就是说,长度N分解到最后为这3个基的组合。此外,由于基-4运算比基-2运算效率更高,也更节省资源,因此基-2的运算量只存在0或1两种可能。
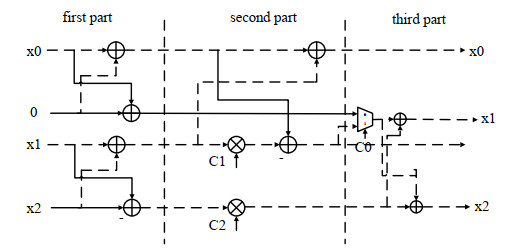 |
| Fig.1 Diagram of radix-3 butterfly circuit 图 1 基-3蝶形电路图 |
| 表 1 控制信号及系数配置 Table 1 Configuration of control signals and coefficients |
另外,综合考虑算法精确度及防止数据溢出等问题,还需要加入缩放因子用以调整幅度。为了简化运算,还需要引入计数器,用以在运算中完成对所有蝶形单元的遍历以及辅助对所有操作数在内存中进行索引。运用以上分解的计算之后,内存中存储的FFT的结果其实是逆序的。需要逆序输出时,可以顺序输出内存中的结果,当需要正序输出时,需要对输出时的读地址进行调整,通过之前的计算依次读取对应的索引号即可完成。
3 算法仿真验证上述算法理论上可支持任意基底的混合基运算,考虑到FPGA资源限制与算法实现难度,这里只实现基-2、基-3、基-4的混合基运算。算法的功能测试在Matlab和Vivado两个平台进行。为了测试算法功能的正确性,首先使用Matlab生成测试数据,然后为了与FPGA平台对比,需要将浮点型数据转换成定点,同时中间计算过程也需要采用定点运算,最后将Matlab与FPGA的结果进行比对。
目前定点DSP对定点数据的处理能力远强于浮点数据,因而在仿真验证中采用Q15量化方案。利用Matlab生成一个载波频率为1×107 Hz与1.2×107 Hz相叠加的双音信号,对该信号做288点FFT运算,分别利用Matlab系统函数、浮点混合基算法以及定点混合基算法进行运算比较。以向量二范数作为表征,可得到标准FFT算法与浮点混合基算法的欧氏距离为6.426 585×10-15,而标准FFT算法与定点混合基算法欧氏距离为3.842 434×10-2。图 2分别给出了浮点混合基算法和定点混合基算法与标准FFT算法绝对误差的比较。从仿真结果可以看出,浮点混合基算法与标准FFT算法可实现精确度的完美拟合,从而验证了算法的可行性。而定点混合基运算存在一定的精确度损失,这一部分损失是由于浮点运算定点化所引入的,由于采用的是Q15的量化方案,存在小数部分的舍位运算,这部分损失可以通过计算得出。在FPGA仿真测试中,混合基FFT算法采用Verilog语言进行编程,运行软件为Vivado 2017.4,输入数据采用Matlab生成的定点数据,利用testbench完成仿真测试。可以看到整个混合基FFT运算一共进行了5级运算,其仿真结果如图 3所示。FPGA最终的定点化运算结果导出至Matlab中进行比对,其与Matlab的定点化运算结果完全一致,从而验证了算法硬件实现的可行性。
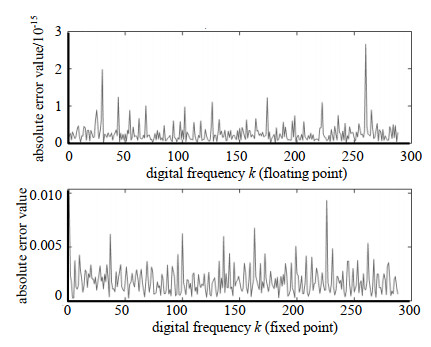 |
| Fig.2 Comparison of absolute errors 图 2 绝对误差对比 |
 |
| Fig.3 Simulation implementation results of the algorithm based on FPGA 图 3 FPGA算法仿真实现结果 |
FPGA实现中算法整体的资源占用情况与固定基知识产权核(Intellectual Property core,IP核)的FFT资源占用对比情况如表 2所示。其中,混合基算法采用288点FFT运算,而固定基算法使用512点FFT运算。可以看到,无论从LUTs, registers, block RAM还是DSPs,混合基所占用的运算资源均小于固定基,因而可以有效节省系统资源。
| 表 2 混合基与固定基运算资源占用对比 Table 2 Comparison of resource occupancy between mixed-radix and fixed-radix operations |
在本论文中,针对需要在Xilinx 7 Series FPGA平台上实现高效FFT运算的需求,利用素数因子分解与库利-图基分解相结合的混合分解模式,并采用通用蝶形单元模块设计的方法,提出了一种可适应不同点数FFT计算的混合基FFT算法,并通过MATLAB与Vivado两个仿真平台验证了算法的可行性。
仿真结果表明,基于新型混合基FFT算法可满足基-2、基-3、基-4的混合基FFT运算,相比较固定基FFT算法,在相同序列长度范围内,混合基FFT可精确计算的序列长度数量大大增加,极大提高了算法的适用性。通过对算法进行优化,在省去了一步旋转因子乘法运算的同时也有效减小了存储空间和运算量。此外,该算法极大提高FFT处理点数的灵活性,并能够有效节省运算资源。
| [1] |
程志鹏, 马琪, 竺红卫. 混合基FFT算法运算量分析[J]. 太赫兹科学与电子信息学报, 2016, 14(6): 925-928. (CHENG Zhipeng, MA Qi, ZHU Hongwei. Computational complexity analysis on mixed-radix FFT[J]. Journal of Terahertz Science and Electronic Information Technology, 2016, 14(6): 925-928.) |
| [2] |
DEMUTH G L. Algorithms for defining mixed radix FFT flow graphs[J]. IEEE Transactions on Acoustics Speech & Signal Processing, 1989, 37(9): 1349-1358. |
| [3] |
JACOBSON A T, TRUONG D N, BAAS B M. The design of a reconfigurable continuous-flow mixed-radix FFT processor[C]// 2009 IEEE International Symposium on Circuits and Systems. Taipei, Taiwan, China: IEEE, 2009.
|
| [4] |
XIAO Hao, PAN An, CHEN Yun, et al. Low-cost reconfigurable VLSI architecture for fast Fourier transform[J]. IEEE Transactions on Consumer Electronics, 2008, 54(4): 1617-1622. DOI:10.1109/TCE.2008.4711210 |
| [5] |
HSIAO C F, CHEN Y, LEE C Y. A generalized mixed-radix algorithm for memory-based FFT processors[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2010, 57(1): 26-30. DOI:10.1109/TCSII.2009.2037262 |
| [6] |
MA Cuimei, XIE Yizhuang, CHEN He, et al. Simplified addressing scheme for mixed radix FFT algorithms[C]// 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Florence, Italy: IEEE, 2014.
|
| [7] |
TRUONG T K, REED I S, LIPES R G, et al. On the application of a fast polynomial transform and the Chinese Remainder Theorem to compute a two-dimensional convolution[J]. IEEE Transactions on Acoustics Speech and Signal Processing, 1981, 29(1): 91-97. DOI:10.1109/TASSP.1981.1163520 |
| [8] |
REISIS D, VLASSOPOULOS N. Conflict-free parallel memory accessing techniques for FFT architectures[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2008, 55(11): 3438-3447. DOI:10.1109/TCSI.2008.924889 |
| [9] |
王非非, 杜伟韬. 一种旋转因子访存优化的FFT算法[J]. 太赫兹科学与电子信息学报, 2011, 9(2): 206-210. (WANG Feifei, DU Weitao. Optimized design of memory access for twiddle factors in FFT algorithm[J]. Journal of Terahertz Science and Electronic Information Technology, 2011, 9(2): 206-210.) |
| [10] |
马翠梅. 低复杂度混合基FFT研究与设计[D]. 北京: 北京理工大学, 2014. (MA Cuimei. Research and design of low complexity mixed base FFT[D]. Beijing: Beijing Polytechnic University, 2014.)
|
 2021, Vol. 19
2021, Vol. 19

