1b. 中国科学院 电磁辐射与探测技术重点实验室,北京 100190;
2. 中国科学院大学 电子电气与通信工程学院,北京 100049
1b. Key Laboratory of Electromagnetic Radiation and Sensing Technology, Chinese Academy of Sciences, Beijing 100190, China;
2. School of Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
多输入多输出(MIMO)雷达近年来得到了越来越多研究学者的关注[1−2],由于其独特的多个发射天线独立发射正交信号并且多个接收天线同时接收信号的特点,其获得了远超过实际阵元数目的观测通道,具有很高的数据获取效率,相比同样孔径的单站雷达系统,远远节约了硬件成本,以空间积累代替时间积累,从而具有缩短积累时间,实现单次快拍成像的优势。
稀布MIMO雷达成像紧随着MIMO成像技术在各领域的发展而发展,因为进一步降低了成本,减小系统复杂度,以尽可能小的成本实现尽可能大的目标,也是各类阵列成像技术走向实用、获得推广的必经之路[3−4]。稀布平面MIMO阵列在实际应用中存在的问题是由于阵列单元间隔大于半波长,阵列方向图出现栅瓣,并且对于阵列的副瓣电平难以控制。本文采用遗传算法对阵列排布进行优化,目的在于去除阵因子方向图栅瓣,降低副瓣。遗传算法在对天线阵列进行优化方面早有研究。文献[5-6]是较早使用遗传算法对稀疏阵列进行优化的实例,文献[7]中提出采用改进遗传算法并结合降维算法优化椭圆环阵列的旁瓣特性,文献[8]提出了一种应用于线性天线阵综合中多目标优化遗传算法,文献[9]针对传统遗传算法在迭代后期容易陷入局部最优的问题,提出采用混沌理论和遗传算法相结合的方法对T形MIMO线阵的低旁瓣进行优化。文献[10]引入距离摄动,同时对发射天线和接收天线进行几何修正,优化稀疏MIMO直线阵列方向图,实现了具有较低的相对旁瓣电平和最大自由度的模式合成。遗传算法对天线阵列性能优化设计的研究已有较长历史,对MIMO线阵的研究也有较多的文献,但是对于平面稀疏MIMO阵列的研究并不多见。本文介绍一种针对平面稀布MIMO天线阵列方向图进行优化的遗传算法,将传统平面阵列收发一体改进为收发分离的MIMO阵列,用两个二维矩阵来对天线单元进行分类以及定位,可优化任意排布的面阵方向图。将此算法进行改进还可用于对一维线性稀布MIMO阵列以及更为复杂的三维空间稀布MIMO阵列方向图进行优化。
1 改进遗传算法遗传算法是模拟生物种群进化过程中优胜劣汰、适者生存法则的全局随机优化算法。类比生物繁衍过程,种群中的大量个体进行基因交叉和基因突变,选择性能优异的后代个体,对保留的个体进行繁殖后代,直到满足需求的个体出现。作为全局性的概率优化算法之一,遗传算法适用范围广,简单易操作,对于解决传统搜索方法中难以处理的复杂非线性问题有着很强的适用性[5]。
本文中的改进遗传算法是在传统一维标准遗传算法的编码方式,种群的生成方法,选择、交叉、变异算子的设计基础上进行改进的二维遗传算法,针对在矩形平面随机分布的稀疏阵列的方向图旁瓣问题进行优化设计,约束条件包括阵元数、阵列孔径和阵元间距。采用实值编码优化变量,将二维平面上的点的横纵坐标对改写成复数的实部和虚部,摒弃了传统的二进制编码方式,这些代表阵元位置的复数构成了个体的二维基因序列。在进行遗传操作前对种群进行预处理,遗传操作结束后还需对种群进行后处理[11]。
1.1 初始种群的生成假定初始种群由M个个体组成,个体的有用基因为阵元数N,其中发射单元数为
| $\left\{ \begin{array}{l} {\rm{s}}{\rm{.t}}{\rm{. }} - L/2 \leqslant {x_n} \leqslant L/2, {\rm{ }} - H/2 \leqslant {y_n} \leqslant H/2 \\ {\rm{ }}\left| {\left. {{x_m} - {x_n}} \right| \geqslant {d_x}} \right. \\ {\rm{ }}\left| {\left. {{y_m} - {y_n}} \right| \geqslant {d_y}} \right. \\ {\rm{ }}m, n \in Z, {\rm{ }}1 \leqslant m, n \leqslant P \times Q, {\rm{ }}m \ne n \\ \end{array} \right.$ | (1) |
式中:
| ${S_x} = L - (P - 1) \times {d_x}$ | (2) |
在这个区间中,P个阵元随机分布。同理,y方向的Q个阵元随机分布的区间为:
| ${S_y} = H - (Q - 1) \times {d_y}$ | (3) |
将个体的产生约束在区间,相比较原始阵列排布空间
| ${\boldsymbol{C}}\left( {m, n} \right) = [(n - 1) \times {d_x} - L/2] + j \times [(m - 1) \times {d_y} - H/2]$ | (4) |
因此,一个满基因个体就可以表示为:
| ${\boldsymbol{G}} = {\boldsymbol{R}} + {\rm{j}}{\boldsymbol{I + C}}$ | (5) |
矩阵G为未稀疏的普通平面阵列,为了得到稀布平面MIMO阵列,还需要对上述个体矩阵G进行两步处理,即阵元稀疏化以及分类。
定义个体的特性矩阵S以及个体稀疏矩阵U,矩阵S是包含3种元素(0, 1, -1)的Q行P列矩阵,0代表满基因个体复数矩阵G中需要去掉的阵元,即稀疏化,对应G中相应位置元素取0得到U中元素,1和−1分别代表发射天线和接收天线阵元,其个数分别为发射天线和接收天线的个数
例如,若个体特性矩阵S为:
| ${\boldsymbol{S}} = \left[ {\begin{array}{*{20}{c}} 1 \\ { - 1} \\ 0 \\ \vdots \\ 1 \end{array}\begin{array}{*{20}{c}} 0&0& \cdots &{ - 1} \\ {}&{}&{}&{} \\ {}& \ddots &{}& \vdots \\ {}&{}&{}&{} \\ {}& \cdots &{}&1 \end{array}} \right]$ | (6) |
则对应的个体稀疏矩阵U为:
| ${\boldsymbol{U}} = \left[ {\begin{array}{*{20}{c}} {{x_{11}} + {\rm{j}}{y_{11}}} \\ {{x_{21}} + {\rm{j}}{y_{21}}} \\ 0 \\ \vdots \\ {{x_{Q1}} + {\rm{j}}{y_{Q1}}} \end{array}\begin{array}{*{20}{c}} 0&0& \cdots &{{x_{1P}} + {\rm{j}}{y_{1P}}} \\ {}&{}&{}&{} \\ {}& \ddots &{}& \vdots \\ {}&{}&{}&{} \\ {}& \cdots &{}&{{x_{QP}} + {\rm{j}}{y_{QP}}} \end{array}} \right]$ | (7) |
多个随机个体组成了种群,个体数量决定了种群的复杂度。与个体相对应,分别定义种群特性矩阵
本文以去除平面稀布MIMO阵列阵因子方向图栅瓣、最小化方向图旁瓣为目标,稀布平面MIMO阵列的优化模型为:
| $\left\{ \begin{array}{l} {\rm{ }}\min \left\{ {\max \left\{ {SLL[{E_{{\rm{MIMO}}}}(\theta , \varphi )]} \right\}} \right\} \\ {\rm{ s}}{\rm{.t}}{\rm{. }} - L/2 \leqslant {x_n} \leqslant L/2, {\rm{ }} - H/2 \leqslant {y_n} \leqslant H/2 \\ \left. {{\rm{ }}\left| {{x_m} - {x_n}} \right.} \right| \geqslant {d_x} \\ {\rm{ }}\left| {\left. {{y_m} - {y_n}} \right| \geqslant {d_y}} \right. \\ {\rm{ }}m, n \in Z, {\rm{ }}1 \leqslant m, {\rm{ }}n \leqslant N, {\rm{ }}m \ne n \\ \end{array} \right.$ | (8) |
式中:
计算平面MIMO阵列方向图时先计算出MIMO阵列的虚拟阵列阵元位置,再用计算普通平面阵列方向图的方法得到原始MIMO阵列的方向图。对于发射单元和接收单元数量分别为
| $\left\{ \begin{array}{l} {x_n} = ({x_{{t_i}}} + {x_{{r_j}}})/2 \\ {y_n} = ({y_{{t_i}}} + {y_{{r_j}}})/2 \\ n = 1, 2, \cdots , {N_{\rm t}} \times {N_{\rm r}} \\ \end{array} \right.$ | (9) |
可以得到MIMO阵列方向图为
| ${E_{{\rm{MIMO}}}}(\theta , \varphi ) = \sum\limits_n {\exp [{\rm{j}}k({x_n}u + {y_n}v)]} $ | (10) |
式中:
个体的适应度为最大旁瓣电平的绝对值,适应度函数值越大则代表性能更优,适应度函数表达式为:
| $fit = |\max \left\{ {SLL[{E_{{\rm{MIMO}}}}(\theta , \varphi )]} \right\}|$ | (11) |
遗传算法与大多数全局优化算法都存在相同的问题,即优化过程容易陷入局部最优并且后期收敛速度变慢。为解决此问题,本文采用一种基于Logistic混沌序列的扰动方法[12]。若优化迭代过程进入长时间的局部最优状态(在此以最优状态经多次迭代后不发生变化为判定准则),则对群体产生一个大的扰动,其表达式如下:
| $\left\{ \begin{gathered} {x_{n + 1}} = {\mu _x}{x_n}({S_x} - {x_n}) \\ {y_{n + 1}} = {\mu _y}{y_n}({S_x} - {y_n}) \\ \end{gathered} \right.$ | (12) |
式中:
容易证明,扰动之后的阵元依旧满足空间约束条件式(1)。对扰动后的群体进行阵元重新排序,排序只针对未被稀疏的元素,将矩阵元素的实部按行从小到大重新排序,将矩阵元素的虚部按列从小到大重新排序后重新组成种群。
对种群进行的遗传操作都在约束区间
| ${\boldsymbol{P}} = {{\boldsymbol{U}}_M} - {{\boldsymbol{C}}_M}$ | (13) |
遗传操作后需将得到的矩阵
| ${{\boldsymbol{U'}}_M} = {\boldsymbol{P'}} + {{\boldsymbol{C'}}_M}$ | (14) |
式中:
遗传操作的选择过程实质是按照某种方法有概率地选择一部分父代个体进入到子代中。赌轮盘法是较为常用的方法,是一种回放式的随机抽样方法,个体被选择从而可以进入下一代继续繁殖的概率等于其适应度函数值占种群适应度函数值的总和的比例。此种方法在一定程度上可以避免优化过程进入局部最优状态,但是选择过程的误差较大。在此采用锦标赛选择方法[13],每次从种群中选出一定数量的个体,从中选择适应度函数值最高的个体进入子代种群之中。重复该操作即可得到新的种群。
在对P进行交叉操作时,依据交叉概率pc选择需要进行操作的个体,在其中选择任意两个(即矩阵P的某两页以及对应的特性矩阵S),随机选择个体的一个或多个非稀疏元素进行交换,即单点交叉或者多点交叉。将得到的两个个体矩阵元素进行排序,排序方法与产生种群扰动后的排序方法相同。
对交叉操作后的子代个体,依据变异概率pm选择需要进行操作的个体,可进行单点变异或者多点变异。在个体中随机选择非稀疏元素,用区间
多次重复上述的遗传操作,即可得到满足需求的后代个体。由于所有的遗传操作都是在进行约束后的种群中进行,得到的子代群体中的基因均满足间隔约束条件,都是可行解。算法流程图如图 1所示。
 |
| Fig.1 Flow chart of algorithm 图 1 算法流程图 |
鉴于稀布MIMO雷达并不局限于平面阵列,此方法亦可应用于一维直线阵列稀布MIMO和三维空间稀布MIMO阵列。对于直线稀布MIMO阵列,其空间自由度为1,在生成种群时位置坐标用实数即可表示,与平面阵列相比,代表种群的矩阵对应地就减少一个维度。三维稀布MIMO阵列与之类似,只是代表种群的矩阵相应要增加一个维度。此时天线单元的位置坐标不再用复数表示,可用一个包含三个元素的数组表示其空间位置。对应的算法复杂度增加,运行时间加长。
2 阵列优化实例本节以22发22收的平面稀布MIMO阵列为例,P=Q=10,稀布率为(22+22)/(10×10)=44%,交叉概率pc=0.8,变异概率pm=0.1,随机五点交叉和三点变异,初始种群个体数为100,工作频率为77 GHz,单元间隔
当阵列规则排布时,发射阵元、接收阵元分布以及虚拟阵列如图 2(a)所示,阵因子方向图如图 2(b)所示,φ=0°, φ=90°两个主平面方向图如图 3所示。可以看出阵列方向图存在大量栅瓣,旁瓣电平为−13.29 dB。
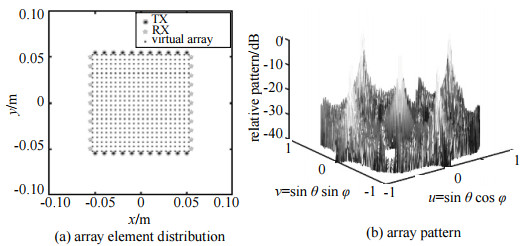 |
| Fig.2 Rectangular MIMO array 图 2 矩形MIMO阵列 |
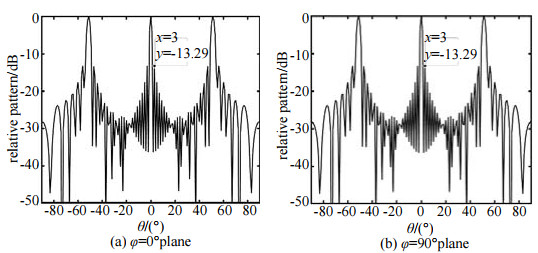 |
| Fig.3 Principal planes pattern 图 3 主平面方向图 |
采用上述改进遗传算法对22发22收平面稀布MIMO阵列进行阵因子方向图优化,表 1中列出采用改进遗传算法对阵列排布进行5次优化分别得到的阵列方向图旁瓣电平最优值。优化后发射阵元、接收阵元分布以及虚拟阵列如图 4(a)所示,阵因子方向图如图 4(b)所示,φ=0°, φ=90°两个主平面方向图如图 5所示。从图中可以看出,优化后阵列排布呈无序排布,阵因子方向图旁瓣消除,方向图旁瓣电平为−16.62 dB,φ=0°平面的方向图旁瓣为−16.87 dB,φ=90°平面的方向图旁瓣为−16.76 dB。同均匀矩形阵列相比,旁瓣电平降低了3.33 dB。
| 表 1 多次优化结果 Table 1 Multiple optimization results |
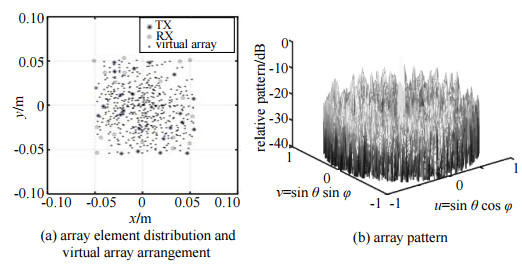 |
| Fig.4 Random arrangement of MIMO array 图 4 随机排布MIMO阵列 |
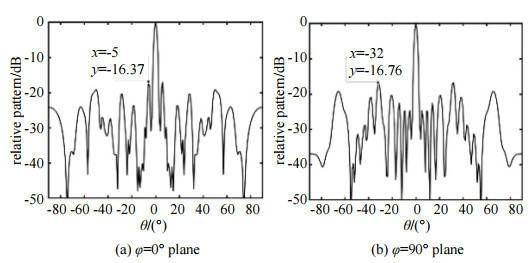 |
| Fig.5 Patterns of principal planes 图 5 主平面方向图: |
将两种稀布MIMO阵列进行成像仿真对比,对距离天线阵列5 m处的点目标进行成像,仿真结果如图 6所示。从图 6(b)可以看出,矩形排布MIMO阵列成像中出现虚假目标,且虚假目标幅度与真实点目标幅度相当,使得无法分辨真假目标。而图 6(c)所示的经过优化后的平面稀布MIMO阵列成像结果,在准确的位置处识别出目标,且不存在虚假目标影响,验证了本文方法的有效性。
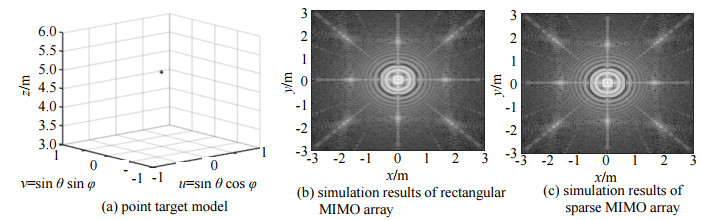 |
| Fig.6 Comparison of point target imaging simulation 图 6 点目标成像仿真对比 |
本文采用改进遗传算法优化稀布平面MIMO阵列方向图,介绍了三维种群矩阵的生成方法,在约束空间中对种群进行遗传操作,减小了算法搜索空间,加快运算速度,采用一种基于Logistic混沌序列的种群扰动方法,使优化迭代过程避免进入局部最优状态。结合具体实例,对比规则排布MIMO阵列和MGA优化后的平面稀布MIMO阵列在阵列方向图和成像性能上的差异,证明了本文提出的方法的优点与可行性,为MIMO雷达的阵列设计提供了参考。此算法还可进一步改进应用于三维空间稀布MIMO阵列的设计。
| [1] |
陈浩文. 一种新兴的雷达体制——MIMO雷达[J]. 电子学报, 2012, 40(6): 1190-1198. (CHEN Haowen. A new radar system——MIMO radar[J]. Acta Electronica Sinica, 2012, 40(6): 1190-1198. DOI:10.3969/j.issn.0372-2112.2012.06.021) |
| [2] |
秦文利, 郑娜娥, 顾帅楠. MIMO雷达弱目标检测前跟踪算法[J]. 太赫兹科学与电子信息学报, 2017, 15(4): 595-600. (QIN Wenli, ZHENG Na-e, GU Shuainan. Tracking algorithm before weak target detection for MIMO radar[J]. Journal of Terahertz Science and Electronic Information Technology, 2017, 15(4): 595-600.) |
| [3] |
陈刚. 稀布阵列MIMO雷达成像技术研究[D]. 南京: 南京理工大学, 2014. (CHEN Gang. Research on sparse array MIMO radar imaging technology[D]. Nanjing, China: Nanjing University of Technology, 2014.)
|
| [4] |
ZHUGE X, YAROVOY A G. Study on two-dimensional sparse MIMO UWB arrays for high resolution near-field imaging[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(9): 4173-4182. DOI:10.1109/TAP.2012.2207031 |
| [5] |
JUNKER G P, KUO S S, CHEN C H. Genetic algorithm optimization of antenna arrays with variable interelement spacings[C]// Antennas & Propagation Society International Symposium. Atlanta, GA, USA: IEEE, 1998.
|
| [6] |
HAUPT R L. Thinned arrays using genetic algorithms[J]. IEEE Transactions on Antennas Propagation, 1994, 42(7): 993-999. DOI:10.1109/8.299602 |
| [7] |
郭睿. 基于修正遗传算法的稀布椭圆环阵列天线综合[D]. 成都: 电子科技大学, 2018. (GUO Rui. Synthesis of sparse elliptical ring array antenna based on modified genetic algorithm[D]. Chengdu, China: University of Electronic Science and Technology, 2018.)
|
| [8] |
HAMMAMI A, GHAYOULA R, GHARSALLAH A. Antenna array synthesis with Chebyshev-genetic algorithm method[C]// International Conference on Communications. Hammamet, Tunisia: IEEE, 2011: 1-4.
|
| [9] |
FU X, CHEN X, HOU Q, et al. An improved chaos genetic algorithm for T-shaped MIMO radar antenna array optimization[J]. International Journal of Antennas Propagation, 2014, 1-6. |
| [10] |
HE Jie, FENG Dazheng, LI Xiaoming, et al. Optimizing thinned antenna array geometry in MIMO radar systems using multiple genetic algorithm[C]// IEEE CIE International Conference on Radar. Chengdu, China: IEEE, 2012: 971-974.
|
| [11] |
陈客松, 稀布天线阵列的优化布阵技术研究[D]. 成都: 电子科技大学, 2006. (CHEN Kesong. Research on optimized array arrangement of sparse antenna array[D]. Chengdu, China: University of Electronic Science and Technology, 2006.)
|
| [12] |
徐洪丽, 钱旭, 岳训, 等. 一种新的基于Logistic混沌映像的自适应混沌蚁群优化算法求解动态车辆路径问题[J]. 计算机应用研究, 2012, 29(6): 2058-2060. (XU Hongli, QIAN Xu, YUE Xun, et al. A new adaptive chaos ant colony optimization algorithm based on Logistic chaos image for dynamic vehicle routing problem[J]. Computer Application Research, 2012, 29(6): 2058-2060. DOI:10.3969/j.issn.1001-3695.2012.06.013) |
| [13] |
张琛. 遗传算法选择策略比较[J]. 计算机工程与设计, 2009, 30(23): 5471-5474. (ZHANG Chen. Comparison of genetic algorithm selection strategies[J]. Computer Engineering and Design, 2009, 30(23): 5471-5474.) |
 2021, Vol. 19
2021, Vol. 19

