区块链技术伴随着数字货币比特币[1]产生,是一个具有全网一致性共识、安全性高防篡改、可编程去中心化等特点的分布式数据账本。区块链技术的核心是构建一个能够自运行且不依赖第三方的社会信任网络,通过所制定的智能合约[2]推动社会来展开价值的量化互联。近年来,区块链技术逐渐从数据货币中抽象出来,随着数字货币的浪潮褪去,其底层支撑平台技术由于不可篡改、不可溯源等特性也受到了越来越多人的关注。区块链在各行各业的应用也成为了区块链发展趋势,目前已经涉及了供应链、物联网、医疗等领域。对于应用层之下的区块链底层技术而言,如何将区块链下沉并深入到硬件的更底层,从而探索更多区块链可能性也是当下热门研究话题。异构计算[3]是一种最能充分利用各种计算资源,使得计算任务的并行性与机器能够有效匹配的分布式计算技术,通过将不同计算类型的任务分配至最合适的计算资源加以执行,从而提高系统整体的资源利用率。当前以硬件电路为基础的异构计算区块链整体上尚在摸索初期,FPGA在区块链方面应用大部分还停留在挖矿阶段,未深入区块链底层结构,暂无成熟的基于FPGA架构的区块链网络,蚂蚁金服在这方面布局较早,也仍然停留在研究阶段,尚未有较成熟成品孵化,在当前硬件区块链发展现状的前提下,区块链计算结构存在着灵活多变的计算任务策略调整,在这方面现场可编程门阵列(FPGA)有着不可替代的优势。本文在此基础上通过云服务器、通用计算机与FPGA搭建区块链异构计算硬件框架,结合相关通信协议和软件算法完善区块链网络结构,为通用计算节点和异构节点分配计算任务并在基础设施上为部署智能合约和执行计算任务提供相应接口,本文的设计方法也可为其他硬件区块链系统的设计提供参考。
1 区块链FPGA节点设计 1.1 区块链FPGA节点概述在区块链系统中,节点是区块链的各个分布式计算中心,由全部节点组成了区块链计算网络。每隔一定时间,由共识算法[4]确定某个区块链节点进行区块打包获得收益。区块打包即该节点向其他节点收集该时间间隔内交易信息,并针对交易进行校验,将校验完毕的交易信息结合区块头等数据打包成一个区块,随后其他节点对该区块进行同步,将新区块链接到现有的区块链上。为了合理设计区块链FPGA节点,首先要确认节点关键数据结构,包括时间戳样式、区块生成时间、区块编号逻辑、区块串联方式、区块统计量参数、交易结构样式等。在数据结构设计完毕后需要对区块链算法结构进行设计,包括节点之间达成一致的共识算法、区块与区块之间串联所用的哈希算法、链上交易所采用的数字签名算法和信息加密解密算法。
1.2 区块与区块链结构设计区块链是由自创世区块开始的一系列区块构成的有向无环链。区块内的数据大部分由交易数据和消息数据构成,因此可以把区块链看作一本交易消息账本,交易是指区块链上账户与账户之间发生的货币转移信息,消息是指区块链上的账户间相互加密通信,交易数据如图 1所示,由于非对称技术的特殊性,每笔交易需要由账户私钥进行签名,并可通过公开的公钥进行验证,而每笔消息需要通过公钥进行加密,由对应接收方的私钥进行解密读取。
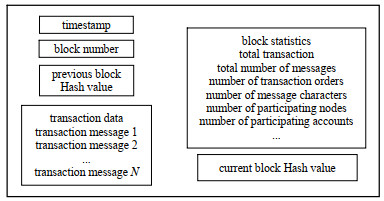 |
| Fig.1 Block parameter 图 1 区块参数 |
区块与区块之间串联成链,每隔一个固定时间完成一次区块生成,生成的区块链接在区块链上,并迅速同步给周边节点。区块与区块之间通过哈希值链接,当前区块的哈希值指向下一个区块,区块链是一条有向无环链,如图 2所示,每个节点均保留一条完整的区块链。
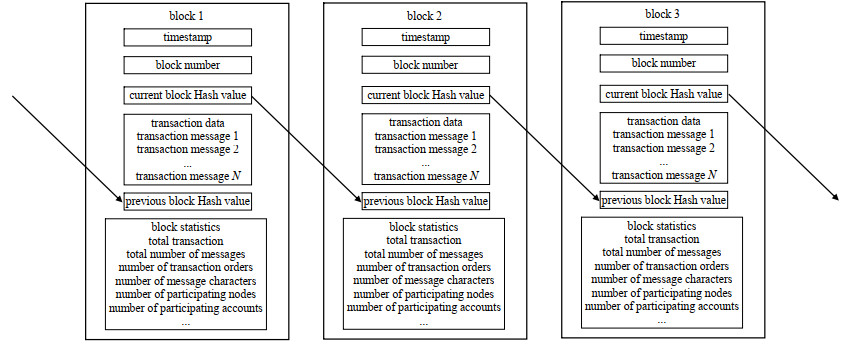 |
| Fig.2 Directed acyclic link of blocks 图 2 区块的有向无环链 |
区块链账户是另一个维度的区块链数据结构,区块链的消息发起、消息接收、资金流动都是归属于账户旗下的,账户通过节点完成相关操作。一个节点可以同时运行多个账户,每个用户也可以拥有多个账户,每个账户独立运行,不受干扰。每一笔交易和消息都与账户相关联。用户通过登录账户来管理数字资产,并在节点上完成对应账户的资产转移和消息收发等操作。在本文设计的体系中,每个账户都有自己的一套私钥、公钥、地址,均不可重复,其中公钥均向外公开,私钥归账户主持有保管,解密消息和交易签名均需要私钥进行处理,公钥可以对消息进行加密、验证签名是否属实。
2 区块链FPGA算法设计 2.1 FPGA算法概述区块链在FPGA上需要实现的算法包含共识算法、哈希算法、非对称加密算法,其中共识算法是为了让区块链的各个节点针对打包权归属与打包利益分配这一事件达成一致性共识;哈希算法是为了通过数字摘要技术让区块链数据进行保护,防止出现数据篡改,同时可让区块通过哈希值指向连接成一条有向无环链;非对称加密算法是通过生成公钥和私钥完成账户之间通信消息通信的加密和解密,对交易的数字签名和验证进行保护。
2.2 非对称加密算法非对称加密算法[5]涉及了两个密钥,公开密钥和私有密钥,二者为一组,在计算过程中通过公钥对内容进行加密,再通过私钥对已加密内容进行解密。公钥和私钥同样可以应用于数字签名,通过私钥对内容进行签名,公钥可验证签名是否属实。与对称加密算法相比,非对称加密算法通常计算结构较复杂,在私钥被妥善保管的情况下安全性较高,难以破解,对称加密技术进行安全通信前,需要以安全方式进行密钥交换,且规模复杂,因此在区块链系统中通常采用非对称加密技术。常见的非对称加密算法包括RSA(Rivest-Shamir-Adleman)、Elgamal、背包算法、Rabin、Diffie-Hellman、椭圆加密算法(Elliptic Curve Cryptography,ECC)等。与其他非对称加密算法相比较,RSA的安全性论据在于大整数分解算法的困难性,目前在数学上未发现任何可用的分解算法,其安全性较高,计算成本适中,对于区块链这类大规模分布式计算匹配程度较高。因此本文采用RSA算法[6]对消息进行加密,并对区块链交易进行签名。
RSA算法包括密钥生成算法、加密算法和解密算法三部分。密钥生成算法步骤如下:
1) 选取两个大质数
2) 计算质数之和:
3) 计算欧拉函数:
4) 随机选取整数
5) 计算
其中,
通过公钥可将信息进行加密,利用加密算法对原文m进行加密,过程如下所示:
密文
密文可通过私钥进行解密得到原文,解密过程如下所示:
原文
数字签名和签名验证过程与加密解密过程类似,签名者通过私钥对消息或交易进行签名后,接受者对已签名的文件通过公钥计算,并将计算结果与原文进行比较,若相同则校验成功,若不同则签名是伪造的或文件发生了篡改。
2.3 共识算法区块链技术运用一套基于共识的数学算法在节点之间建立信任网络,协调保证分布式网络中各节点数据记录一致性。区块链中存在3种经典共识算法,分别是工作量证明算法(Proof of Work,PoW)、股权权益证明算法(Proof of Stake,PoS)、权益委托证明算法(Delegated Proof of Stake,DPoS),为解决对无效和恶意节点数容忍度的问题,出现了实用拜占庭容错(Practical Byzantine Fault Tolerance,PBFT)共识算法[7]。
PoW是工作量证明算法[8],也就是俗称的“挖矿”,各个节点通过算力解题竞争新区块,存在着算力浪费和对现实中的电力、机器造成大量损耗的问题,因此PoS应运而生。PoS是一种根据持有人持有货币的量和时间进行利息分配的制度,PoS机制最核心的逻辑就是通过权益持有者来代替PoW里的矿工,缺点在于无法对恶意节点进行有效规避,在运行初期容易产生节点间权益分配不均的问题。DPoS[9]是基于PoW和PoS的基础上,出现的一种基于投票选举的共识算法。PBFT算法通过解决无效和恶意节点的问题从而提升了系统的稳定性,但在联盟链等应用场景下,存在着通信开销较大,效率低等问题。
本文基于信用分级将PoS与PBFT相结合,设计了一种基于PBFT改进的信用权益分配算法,简称为C-PoSBFT(Credit Proof of Stake Byzantine Fault Tolerance),该算法能够通过信用积分制度减少传统PBFT算法的通信开销,提升系统整体效率。与PoS相比,C-PoSBFT能够对恶意节点进行有效规避,保证区块链系统的稳定运行且收益分配合理。在新区块生成前,首先对每个节点进行账户统计,得到每个节点与节点当前登陆账户的对应关系,再分别对每个账户进行权益计算。每个账户的权益由该账户当前账面余额与该余额对应各个部分存续时间的乘积,FPGA内时间精确度较高,可取得时间精确度为
基于节点权益情况和节点过往执行行为,计算信用积分并对节点进行信用分级,以节点权益情况作为初始积分,节点作为主节点打包区块获得大量点信用积分,作为从节点每参与一次有效区块生成则获取少量点信用积分,未生成有效区块则扣除大量点信用积分。信用级别分为
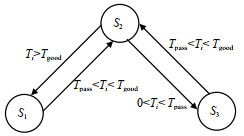 |
| Fig.3 State transition of node credit level 图 3 节点信用级别状态转换 |
在三种不同的节点信用级别状态下,存在着不同的节点权限,只有信用级别为
哈希计算[10]是一种压缩映射转换过程,通过将一段任意长度的输入,经过哈希算法压缩成某一固定长度的消息摘要。常用的哈希算法包括第五版消息摘要算法(Message-Digest Algorithm 5,MD5)、安全散列算法1 (Secure Hash Algorithm-1,SHA-1)、长度256的安全散列算法(Secure Hash Algorithm-256,SHA-256)等。本文采用了安全散列算法SHA-256为区块数据结构做映射,通过该算法将区块数据摘要转换为32个字节的数组,即256 bit的哈希值。
在计算前首先要进行常量初始化,对自然数中的前8个质数的平方根的小数部分取前32位可得到SHA-256算法中的8个哈希初值,同样,对自然数中前64个质数的立方根的小数部分取前32 bit可得到哈希常量。消息在计算前需要进行预处理,包括附加填充比特和附加长度值。在哈希计算过程中,首先将信号分解成n个512位的块,再将哈希初值与各个块依次结合进行共n次迭代,迭代完成则得到最终哈希值。计算过程如下所示:
1) 初始化:
2) 消息列表:
| ${W_t} = \sigma _1^{\left\{ {256} \right\}}\left( {{W_{t - 2}}} \right) + {W_{t - 7}} + \sigma _0^{\left\{ {256} \right\}}\left( {{W_{t - 15}}} \right) + {W_{t - 16}}$ | (1) |
3) 对于
| ${T_1} = h + \mathop \sum \nolimits_1^{\left\{ {256} \right\}} \left( e \right) + Ch\left( {e, f, g} \right) + K_t^{\left( {256} \right)} + {W_t}$ | (2) |
| ${T_2} = \mathop \sum \nolimits_0^{\left\{ {256} \right\}} \left( a \right) + {M_{aj}}\left( {a, b, c} \right)$ | (3) |
式中:
4) 计算中间散列值,第
上述算法中的6个逻辑函数如下:
| $\mathop \sum \nolimits_0^{\left\{ {256} \right\}} \left( x \right) = ROT{R^2}\left( x \right)POT{R^{13}}\left( x \right) \oplus ROT{R^{22}}\left( x \right)$ |
| $\mathop \sum \nolimits_1^{\left\{ {256} \right\}} \left( x \right) = ROT{R^6}\left( x \right)POT{R^{11}}\left( x \right) \oplus ROT{R^{25}}\left( x \right)$ |
| $ {\sigma }_{0}^{\left\{256\right\}}=ROT{R}^{7}\left(x\right)\oplus POT{R}^{18}\left(x\right)\oplus ROT{R}^{3}\left(x\right)$ |
| $\sigma _1^{\left\{ {256} \right\}} = ROT{R^{17}}\left( x \right) \oplus POT{R^{19}}\left( x \right) \oplus ROT{R^{10}}\left( x \right)$ |
随着数字浪潮的褪去,区块链技术逐渐从数字货币中抽象出来,其底层支撑平台由于可溯源[11]、不可篡改等特性受到了越来越多的关注,区块链底层平台的研发也成为了区块链重要发展方向之一。在传统结构中,区块链通常部署在以CPU和GPU为核心的通用计算机上,并将区块数据存储在硬盘中。随着区块链技术的不断发展,区块链与其他行业不断融合,对系统的计算效能、功耗、兼容性都有更高要求。整体上硬件区块链[12]尚在发展初期,与各个行业的应用也在不断探索,在计算效能的基础上需要灵活多变的计算任务和计算策略予以支持,区块链是一种通信密集型和计算密集型业务,通过将通用处理器与FPGA相结合能够得到稳定且极低的延迟和较低的功耗。随着区块链计算网络的布设,系统逐渐扩大,通用计算机和云服务器以及之间的通信链路会带来更高的延迟和计算效能的降低,但与传统的区块链系统的通用计算机结合云服务器架构相比,FPGA同时拥有流水线并行和数据并行,而CPU/GPU流水线深度受限,几乎只存在数据并行,例如处理一个数据包存在5个步骤,FPGA可通过5级流水线,在流水线的不同级处理不同的数据包,而CPU/GPU的数据并行是通过5个计算单元来保持同步调,以单指令多数据流(Single Instruction Multiple Data,SIMD)方式实现。当计算任务是逐个而非成批到达时,流水线并行比数据并行可实现更低的计算延迟,因此对流式计算的任务,FPGA计算比CPU/GPU有着架构层面的延迟和效能方面的优势。本文中的异构计算区块链系统中FPGA部分与通用计算结构相比较,其计算效能具有数量级层面上的优势。在整体系统计算资源中,搭配合理情况下,FPGA占比越高,则提升越明显,除去性能优化外,在区块链向硬件领域下沉的发展维度上来看,该方案为区块链的未来应用拓展探索了更多的可能性。
| 表 1 流式计算任务在不同体系下的性能比较 Table 1 Performance comparison of streaming computing tasks under different systems |
异构计算通过按任务类型进行分工,将专用问题和通用问题区分开来,专业问题涉及的计算任务包括非对称计算、哈希计算、区块打包及共识计算;通用问题涉及的计算任务主要针对区块链底层平台向服务层提供的接口,通过接口搭建区块链上层应用,通过将不同计算类型的子任务分配到最合适的计算资源加以执行,能够有效地提高计算效率。这里将涉及到应用层的通用问题分配给CPU和GPU进行执行,将非对称计算、哈希计算、区块打包及共识计算这些专用问题分配给FPGA进行执行,并通过串口将FPGA打包好的区块发送至通用计算机进行存储。在本文设计中,采用了基于冯·诺依曼结构的CPU和GPU与半定制FPGA电路组成不同指令集和体系架构的异构计算网络,从而经济有效地获得高性能计算能力、优秀的兼容性和可拓展性以及较高的计算资源利用率。
3.2 计算系统设计本文中一个完整的异构计算系统包括通用计算机、云服务器和FPGA阵列三部分,如图 4所示,由于节点间需要对交易消息进行实时数据同步,因此在系统中需要围绕这三部分进行通信链路构建,包括通用计算机与FPGA之间、FPGA与FPGA之间,通用计算机和云服务器之间,同时针对未来实际应用中可能接入大量FPGA阵列,需要留下足够的接口空间保证异构区块链的可拓展性。在一个区块周期内,交易和消息在各个节点记录,当周期结束时,对应的节点需要从其他节点通过通信同步这些数据,并在区块生成后由该节点进行分发通信,在指定位置进行分布式存储。
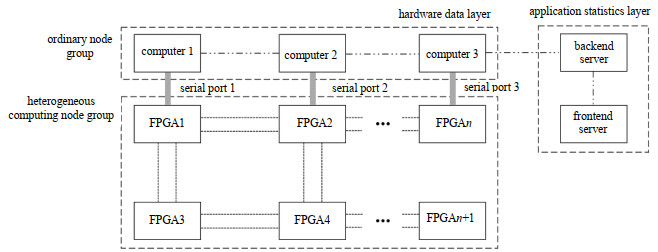 |
| Fig.4 Framework of the heterogeneous computing blockchain system 图 4 异构计算区块链系统框架 |
FPGA之间采用了美国电子工业协会推荐标准485(Recommend Standard-485,RS-485)串行通信标准[13],采用差分传输方式进行通信,与美国电子工业协会推荐标准232[14](Recommend Standard-232,RS-232)这类单线通信方式相比,该通信方式能够有效减少噪声引起的干扰,传输距离较长,能够在总线上通过连接多个收发器同时进行多块FPGA之间的通信。利用每个单一的RS-485接口建立起多设备网络,再通过链接多个RS-485接口建立更复杂的通信网络结构,结构中的数据传输速率最高能达到10 Mbps,能够有效解决硬件区块链上的信息传递需求。整体电路采用了1.2 V, 2.5 V, 3.3 V这三种电压,通过电压转换芯片将5 V电压分压得到。
本文硬件区块链系统中的FPGA与本地计算机之间采用通用串行总线(Universal Serial Bus,USB)转晶体管-晶体管逻辑电平(Transistor-Transistor Logic,TTL)方案[15],利用CH340芯片实现USB总线转通用异步收发传输器(Universal Asynchronous Receiver/Transmitter,UART)功能,采用Mini USB接口与通用计算机进行通信。串口采用5 V电压和12 MHz晶振作为输入,通过TXD和RXD接口与FPGA相连,进行信号的传递与接收。
在硬件电路的基础上,需要通过编写串口通信协议[16]并烧写至FPGA内串口转USB完成信息发送及接收功能,由Verilog程序转化得到的电路网表文件顶层模块的内容包括:uart_recv是串口接收模块,从串口接收端口uart_rxd接收上位机发送的串行数据,并在一帧数据接收结束后给出通知信号uart_done。uart_done为发送使能信号,将接收到的数据uart_data通过串口发送端口uart_txd发送出去。
本文中的FPGA之间的基于RS-485编写的通信协议电路网表文件顶层模块包括4个模块,通过数据控制模块data_control管理待发送的数据;通过uart_send完成数据发送功能;通过uart_recv完成数据接收功能;通过key_data完成数据标志位提示功能,在顶层模块完成了上述4个模块的实例化,设置数据位为8位,停止位为1位,无校验位,波特率为115 200 bps。由Modelsim可得代码仿真波形如图 5所示,波形包括了分频计数、串口收发、标志位、计算结果和中间量等,在时域上通过各个信号相互作用实现区块链相关功能。
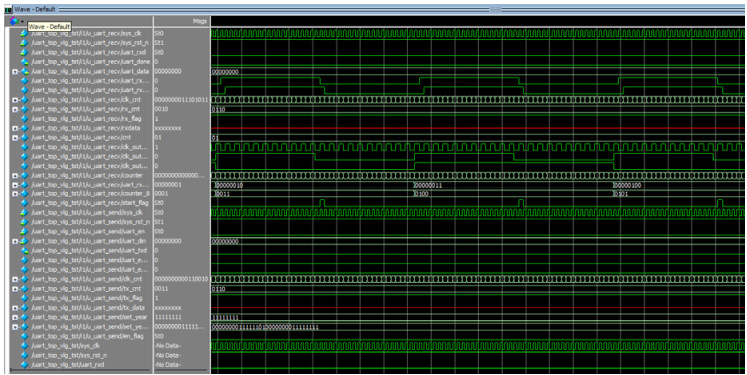 |
| Fig.5 Simulation waveform of the blockchain circuit 图 5 区块链电路仿真波形 |
每台本地计算机、云服务器和FPGA均作为一个区块链节点,对区块链行为进行加速计算,组成一个完整的区块链系统,其中FPGA作为异构计算节点,在其中可完成非对称计算、哈希计算、区块生成及共识计算,在各个节点中发生交易时,交易发起的账户需要通过私钥进行数字签名[17],该签名可被对应的公钥进行验证,在节点验证成功后,对交易数据进行记录,并将交易数据发送至本地计算机进行记录存储。
每到区块打包时间前,首先通过共识算法计算得出获得区块打包权益的节点,对该节点上的打包对应账户发放区块打包权益,随后该节点在各个节点间同步该时间段内各个节点上的交易信息,将交易信息通过SHA-256算法进行哈希计算得出哈希值,并将上一个区块的哈希值保留,保持区块链串联结构,将打包好的区块通过通信网络同步给其他节点,并通过串口将打包好的区块特征值发送至本地计算机进行展示以及存储,可在本地计算机上通过串口调试助手观察接收到的信息,串口数据如图 6所示,包括了交易信息和区块打包信息。
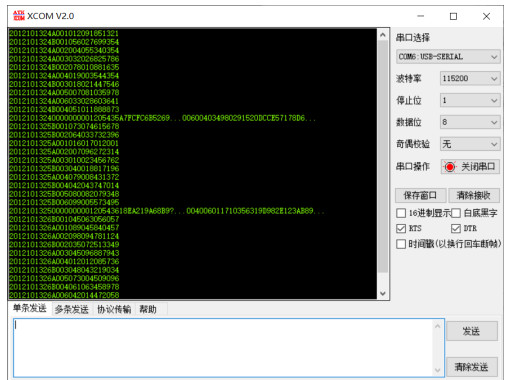 |
| Fig.6 Information of transaction and block packaging 图 6 交易与区块打包信息 |
区块链技术由于其分布式计算[18]、可溯源、不可篡改和公开透明等特性正在对传统行业技术进行革新和颠覆,发展速度日新月异,在数字货币金融、供应链、医疗、资产管理、选举投票等方面已经有着较为广泛的应用。目前区块链的发展时间较短,在计算效能等方面仍存在着可提升的空间。
本文将FPGA与通用计算机结合,通过异构计算设计了一套硬件区块链系统。在对计算需求和通信需求进行分析的基础上,利用RS-485串口通信协议[19]和USB转TTL方案搭建了FPGA与FPGA之间、FPGA与本地计算机之间的通信框架。将FPGA作为区块链的计算节点,通过FPGA阵列组成节点阵列起到分布式计算枢纽的作用,以节点为单位支撑区块链网络的运行流转,完成交易消息发起、共识计算、非对称加密与解密[20]、数字签名与验证、哈希计算、区块组链等功能。整体设计以分布式计算为基础,在FPGA和通用计算机组网中搭建了区块链各类特性,从而构成了完备的硬件区块链网络。
区块链技术从数字货币出发,与其他行业相结合已经是当下区块链的热门发展方向。搭建在以CPU和GPU为核心的通用计算机上的传统区块链已经广泛应用于各行各业,在区块链与行业结合不断深入的过程中,在大规模部署的情况下,其对计算效能、功耗等要求越来越高,CPU和GPU受限于冯·诺依曼结构,在获得较高的通用计算能力的同时,也存在着计算效能和功耗等方面的短板。异构计算利用不同计算类型的资源相互协调分配工作从而可在最短时间内完成相应的计算任务,搭建异构计算硬件区块链系统能够让区块链向硬件底层结构不断延伸,在行业应用和技术探索方面有着更灵活的计算架构调整策略,从而获得更多的发展可能。
本文中区块链通信结构搭建、区块打包等区块链核心机制设计和FPGA算法部分主要由徐易朗负责,通用处理器和云服务器计算部分主要由毕涛负责,赵建业教授负责本文的方向指导并统领全文进行修改。
| [1] |
NAKAMOTO Satoshi. Bitcoin: a peer-to-peer electronic cash system[R]. 2008: 1-9.
|
| [2] |
CHRISTIDIS Konstantinos, DEVETSIKIOTIS Michael. Blockchains and smart contracts for the internet of things[J]. IEEE Access, 2016, 4: 2292-2303. DOI:10.1109/ACCESS.2016.2566339 |
| [3] |
TOPCUOGLU H, HARIRI S, WU M Y. Performance-effective and low-complexity task scheduling for heterogeneous computing[J]. IEEE Transactions on Parallel and Distributed Systems, 2002, 13(3): 260-274. DOI:10.1109/71.993206 |
| [4] |
袁勇, 倪晓春, 曾帅, 等. 区块链共识算法的发展现状与展望[J]. 自动化学报, 2018, 44(11): 2011-2022. (YUAN Yong, NI Xiaochun, ZENG Shuai, et al. Blockchain consensus algorithms: the state of the art and future trends[J]. Acta Automatica Sinica, 2018, 44(11): 2011-2022.) |
| [5] |
SIMMONS G J. Symmetric and asymmetric encryption[J]. ACM Computing Surveys, 1979, 11(4): 305-330. DOI:10.1145/356789.356793 |
| [6] |
暴金雨. RSA公钥密码体制的原理及应用[J]. 科技传播, 2019, 11(6): 137-139. (BAO Jinyu. Principle and application of RSA public key cryptosystem[J]. Public Communication of Science & Technology, 2019, 11(6): 137-139. DOI:10.3969/j.issn.1674-6708.2019.06.083) |
| [7] |
SUKHWANI H, MARTÍNEZ J M, CHANG X, et al. Performance modeling of PBFT consensus process for permissioned blockchain network(hyperledger fabric)[C]// 2017 IEEE 36th Symposium on Reliable Distributed Systems(SRDS). Hong Kong, China: IEEE, 2017: 253-255.
|
| [8] |
韩璇, 刘亚敏. 区块链技术中的共识机制研究[J]. 信息网络安全, 2017, 17(9): 147-152. (HAN Xuan, LIU Yamin. Research on the consensus mechanisms of blockchain technology[J]. Netinfo Security, 2017, 17(9): 147-152. DOI:10.3969/j.issn.1671-1122.2017.09.034) |
| [9] |
LUO Y, CHEN Y, CHEN Q, et al. A new election algorithm for DPos consensus mechanism in blockchain[C]// 2018 7th International Conference on Digital Home(ICDH). Guilin, China: IEEE, 2018: 116-120.
|
| [10] |
TING K K, YUEN S C L, LEE K H, et al. An FPGA based SHA-256 processor[C]// International Conference on Field Programmable Logic and Applications. Heidelberg, Berlin: Springer, 2002: 577-585.
|
| [11] |
郭珊珊. 供应链的可信溯源查询在区块链上的实现[D]. 大连: 大连海事大学, 2017. (GUO Shanshan. Realization of trusted traceability query of supply chain on blockchain[D]. Dalian, China: Dalian Maritime University, 2017.)
|
| [12] |
FLORIN R, IONUT R. FPGA based architecture for securing IoT with blockchain[C]// 2019 International Conference on Speech Technology and Human-Computer Dialogue(SpeD). Timisoara, Romania: IEEE, 2019.
|
| [13] |
耿立中, 王鹏, 马骋, 等. RS485高速数据传输协议的设计与实现[J]. 清华大学学报(自然科学版), 2008, 48(8): 1311-1314. (GENG Lizhong, WANG Peng, MA Cheng, et al. Design and implement of RS485 high speed data communications protocol[J]. Journal of Tsinghua University(Science and Technology), 2008, 48(8): 1311-1314. DOI:10.3321/j.issn:1000-0054.2008.08.022) |
| [14] |
邢庭炜. RS232串口通信在PC机与单片机通信中的应用[J]. 信息系统工程, 2016(8): 110-111. (XING Tingwei. Application of RS232 serial port in communication between PC and MCU[J]. China CIO News, 2016(8): 110-111. DOI:10.3969/j.issn.1001-2362.2016.08.082) |
| [15] |
许波, 赵佳. 一种FPGA与PC通信方法及其应用[J]. 电子测量技术, 2018, 41(2): 115-118. (XU Bo, ZHAO Jia. Method of communication between FPGA and PC and its application[J]. Electronic Measurement Technology, 2018, 41(2): 115-118.) |
| [16] |
党俊博, 李哲, 李雅俊. 基于FPGA的串口通信电路设计与实现[J]. 电子科技, 2016, 29(7): 106-109. (DANG Junbo, LI Zhe, LI Yajun. Design and implementation of serial communication circuits based on FPGA[J]. Electronic Science and Technology, 2016, 29(7): 106-109.) |
| [17] |
张先红. 数字签名原理及技术[M]. 北京: 机械工业出版社, 2004. (ZHANG Xianhong. Principle and technology of digital signature[M]. Beijing: China Machine Press, 2004.)
|
| [18] |
谢文武, 吴宇, 朱鹏, 等. 一种基于FPGA的分布式计算的实现方法及系统: CN109976912A[P]. 2019. (XIE Wenwu, WU Yu, ZHU Peng, et al. A method and system for realizing distributed computing based on FPGA: CN109976912A[P]. 2019.)
|
| [19] |
李超, 庄伟, 颜敏. 一种抗辐照试验测试系统中RS485总线IO卡设计[J]. 太赫兹科学与电子信息学报, 2017, 15(2): 333-337. (LI Chao, ZHUANG Wei, YAN Min. Design of a RS485 bus IO card applied in measurement system of anti-radiation experiment[J]. Journal of Terahertz Science and Electronic Information Technology, 2017, 15(2): 333-337.) |
| [20] |
张建莉. RSA加密算法加密与解密过程解析[J]. 农业网络信息, 2017(4): 106-108. (ZHANG Jianli. Analysis on the encryption and decryption process of RSA encryption algorithm[J]. Agriculture Network Information, 2017(4): 106-108.) |
 2021, Vol. 19
2021, Vol. 19


