随着无线传感网络(WSN)的广泛使用,其已成为监测如智能电网[1]、铁路/公路[2]、生产/制造[3]等关键基础设施的重要手段。而异常流量的检测活动,如入侵,对于关键基础设施的长期连续监测起着至关重要的作用。当前常用的入侵检测方案有数据挖掘、博弈理论、流量预测、计算智能等。文献[4]采用免疫理论中的阴性选择算法实现对WSN入侵活动的监测。文献[5]采用K-means聚类算法对WSN所采集的大量数据进行训练及分类来检测各类入侵攻击。文献[6]提出一种基于博弈论的入侵检测系统,用于有效检测WSN中的异常数据流。文献[7]提出一种基于簇结构的混合入侵检测系统(Clustered Hierarchical Hybrid-Intrusion Detection System,CHH-IDS),该方案可以同时检测已知攻击和未知攻击,同时分析了数据流对入侵检测准确率的影响。文献[8]采用基于核自组织映射和粒子群优化(Kernel Self-Organizing Map and Particle Warm Optimization,KSOM-PSO)的神经网络对WSN进行入侵检测,可大幅提高入侵检测精确度。文献[9]提出一种WSN多阶段动态入侵检测博弈模型,主要利用贝叶斯规则修正下一阶段节点的后验概率,可明显提高簇形WSN的入侵检测准确率。文献[10]提出一种结合信任机制和噪声检测技术的多协议层入侵检测(Trust-based Multi-Protocol layer Noise Intrusion Detection,T-MPNID)方法,用以解决跨层攻击检测中的高误报率和漏报率。目前多数入侵检测算法主要基于数据挖掘算法[11],采用该类方案的WSN监测系统具有较好的入侵检测性能,但仍易遭受各类潜在的安全威胁和未知攻击,需要构建有效的入侵检测系统(Intrusion Detection System,IDS),避免所采集的数据受已知和未知攻击,即通过检测异常活动提高WSN安全是建立IDS的根本目的[12-13]。识别WSN中异常活动的有效策略有机器学习、模糊逻辑、人工神经网络等。IDS作为一种主动防御计算,主要通过二值分类区分正常行为和入侵行为,其中实施入侵检测的关键在于如何决定子系统的融合数据流。
因此,针对基于WSN的关键基础设施监测系统,通过分析WSN在感测数据融合阶段已知和未知的入侵行为,本文提出一种WSN数据融合阶段的自适应入侵检测方案(Adaptive Intrusion Detection scheme in Data Fusion Stage,AID-DFS)。方案首先利用两类机器学习子系统对数据进行处理:a)异常检测子系统(Anomaly Detection Subsystem,ADS),主要用于检测未知攻击,其基本原理是利用优化的DBSCAN分类器根据训练数据先获取非攻击模型,再比较感测数据来识别未知攻击;b)误用检测子系统(Misuse Detection Subsystem,MDS),主要用于检测已知攻击,其基本原理是利用随机森林分类器根据训练数据先获得攻击模型,再利用未来感测流量识别入侵行为。通过连续跟踪2个子系统的接收操作特征(ROC)以及结合ROC奖惩机制,从而实现自动调整转发至每个子系统的融合数据比例。与其他经典入侵检测方案相比,AID-DFS方案的入侵检测准确率可高达99.6%,入侵检测率可高达94.9%。
1 网络模型AID-DFS方案采用簇化网络结构,见图 1。假设无线传感网络被划分成n个簇,每个簇包含c个节点,则一个簇的节点集可表示为:
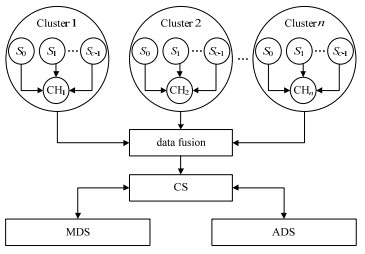 |
| Fig.1 Network model of the AID-DFS scheme 图 1 AID-DFS方案网络模型 |
AID-DFS方案的簇头选举方法采用基于权重的簇头产生机制[6],即首先按照式(1)给出的权重计算方法,簇内每个节点都计算出其各自的簇头权重,然后再比较各节点的权重大小,最后选举权重最低的节点作为该簇的簇头。
| ${W_j} = {\omega _1}\Delta j + \frac{{{\omega _2}}}{{\left| {1/SRS{S_j}} \right|}} + {\omega _3}{M_j} + {\omega _4}{\tau _j}$ | (1) |
式中:Wj为节点Sj的权重;ω1, ω2, ω3与ω4为式中各项的权重系数;
各簇选举出簇头后,簇头将簇内各成员节点的数据进行融合,并把融合后的数据传递至基站。AID-DFS采用文献[7]中的融合算法计算融合节点的信任分,如式(2)所示:
| ${T_{\rm{agg}}} = \frac{{\left( {\sum\limits_{j = 0}^{c - 1} {\left( {{T_j} + 1} \right) \times T_{\rm{agg}}^j} } \right)}}{{\sum\limits_{j = 0}^{c - 1} {\left( {{T_j} + 1} \right)} }}$ | (2) |
式中:Tj为Sj的信任值;
AID-DFS主要思路:首先,分别计算异常检测子系统和误用检测子系统在任意时刻的ROC;然后,跟踪2个子系统的ROC变化,计算出决策函数;最后,根据决策函数实现动态调整向2个子系统转发融合数据的比例。
1) 分别确定2个子系统在ti时刻的ROC(即真假率)。其中,真假率的定义为真阳率(True Positive,TP)与假阳率(False Positive,FP)之比,如式(3)所示:
| $\left\{ \begin{gathered} {M_{{\rm{ADS}}}}\left( {{t_i}} \right) = \frac{{{P_{{\rm{T, ADS}}}}\left( {{t_i}} \right)}}{{{P_{{\rm{F, ADS}}}}\left( {{t_i}} \right)}} \\ {M_{{\rm{MDS}}}}\left( {{t_i}} \right) = \frac{{{P_{{\rm{T, MDS}}}}\left( {{t_i}} \right)}}{{{P_{{\rm{F, MDS}}}}\left( {{t_i}} \right)}} \\ \end{gathered} \right.$ | (3) |
式中:
| $\left\{ \begin{gathered} {M_{{\rm{ADS}}}}\left( {\Delta t} \right) = \frac{{{P_{{\rm{T, ADS}}}}\left( {\Delta t} \right)}}{{{P_{{\rm{F, ADS}}}}\left( {\Delta t} \right)}} \\ {M_{{\rm{MDS}}}}\left( {\Delta t} \right) = \frac{{{P_{{\rm{T, MDS}}}}\left( {\Delta t} \right)}}{{{P_{{\rm{F, MDS}}}}\left( {\Delta t} \right)}} \\ \end{gathered} \right.$ | (4) |
式中
| $\left\{ \begin{gathered} {M_{{\rm{ADS}}}}\left( {{t_{i + 1}}} \right) = \alpha {M_{{\rm{ADS}}}}\left( {{t_i}} \right) + \left( {1 - \alpha } \right){M_{{\rm{ADS}}}}\left( {\Delta t} \right) \\ {M_{{\rm{MDS}}}}\left( {{t_{i + 1}}} \right) = \alpha {M_{{\rm{MDS}}}}\left( {{t_i}} \right) + \left( {1 - \alpha } \right){M_{{\rm{MDS}}}}\left( {\Delta t} \right) \\ \end{gathered} \right.$ | (5) |
式中α为权重参数。
2) AID-DFS跟踪异常检测子系统和误用检测子系统中的接收操作特征,计算出任意时刻ti的决策函数
| $I\left( {{t_i}} \right) = \frac{{{M_{{\rm{ADS}}}}\left( {{t_i}} \right)}}{{{M_{{\rm{MDS}}}}\left( {{t_i}} \right)}}$ | (6) |
如果
| $\left\{ {\begin{array}{*{20}{c}} {{R_{\rm{a}}}\left( {{t_{i + 1}}} \right) = {R_{\rm{a}}}\left( {{t_i}} \right) + \Delta R} \\ {{R_{\rm{m}}}\left( {{t_{i + 1}}} \right) = {R_{\rm{m}}}\left( {{t_i}} \right) - \Delta R} \end{array}} \right.$ | (7) |
反之,则说明误用检测子系统优先于异常检测子系统,此时应增加向误用检测子系统转发融合数据的比例。即增加
| $\left\{ {\begin{array}{*{20}{c}} {{R_{\rm{a}}}\left( {{t_{i + 1}}} \right) = {R_{\rm{a}}}\left( {{t_i}} \right) - \Delta R} \\ {{R_{\rm{m}}}\left( {{t_{i + 1}}} \right) = {R_{\rm{m}}}\left( {{t_i}} \right){\rm{ + }}\Delta R} \end{array}} \right.$ | (8) |
式中:
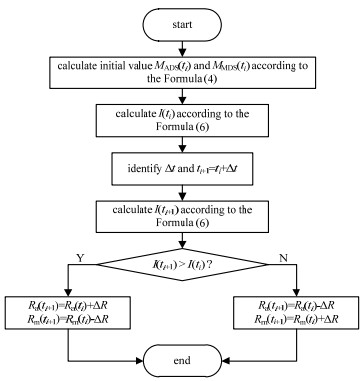 |
| Fig.2 Intrusion detection flow of the AID-DFS 图 2 AID-DFS方案入侵检测流程图 |
AID-DFS采用NS3仿真器进行仿真验证。仿真无线传感器网络包含25个节点,随机部署在100 m×100 m的区域内,网络被划分为4个簇,节点间的通信采用层次-动态源路由协议。采用KDD CUP 1999数据库对AID-DFS、CHH-IDS、KSOM-PSO和T-MPNID进行性能分析比较。仿真无线传感器网络的其他参数如表 1所示。
| 表 1 仿真参数 Table 1 Simulation parameters |
准确率(Accuracy Rate,AR)是指能够准确区分不同入侵攻击类型的概率:
| $R_{\mathrm{A}}=\frac{P_{\mathrm{T}}+N_{\mathrm{T}}}{P_{\mathrm{T}}+N_{\mathrm{T}}+P_{\mathrm{F}}+N_{\mathrm{F}}}$ | (9) |
式中:NF为假阴率;NT为真阴率。
图 3给出了随着入侵率的增加,AID-DFS, CHH-IDS, KSOM-PSO与T-MPNID方案检测入侵类型的准确率变化情况,其中ΔR=0.25。由图 3可以看出,随着网络入侵率的增加,4种方案检测入侵类型的准确率均呈现下降趋势,CHH-IDS检测入侵类型的准确率下降幅度最快。当入侵率为20%时,CHH-IDS检测入侵类型的准确率为99.7%,KSOM-PSO检测入侵类型的准确率为99.76%,T-MPNID检测入侵类型的准确率为99.83%,而AID-DFS方案检测入侵类型的准确率可高达99.9%;当入侵率为50%时,CHH-IDS检测入侵类型的准确率已经降到99.1%,KSOM-PSO检测入侵类型的准确率为99.23%,T-MPNID方案检测入侵类型的准确率为99.42%,而AID-DFS检测入侵类型的准确率仍可高达99.6%。
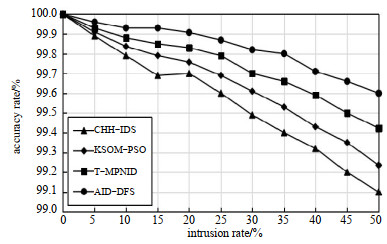 |
| Fig.3 Comparison of intrusion detection accuracy among four schemes 图 3 4种方案的入侵检测准确率比较 |
检测率(Detection Rate,DR)是指能够正确检测出入侵的概率:
| $R_{\mathrm{D}}=\frac{P_{\mathrm{T}}}{P_{\mathrm{T}}+P_{F}}$ | (10) |
图 4给出了随着入侵率的增加,AID-DFS, CHH-IDS, KSOM-PSO与T-MPNID的检测率变化情况。由图 4可以看出,随着入侵率的增加,4种方案的检测率均呈现下降趋势,其中CHH-IDS检测率下降幅度更快。当入侵率为30%时,CHH-IDS的检测率为93.6%,KSOM-PSO的检测率为94.4%,T-MPNID的检测率为95.3%,而AID-DFS方案的检测率可达到96.5%;当入侵率为50%时,CHH-IDS的检测率为84.7%,KSOM-PSO的检测率为88.9%,T-MPNID的检测率为91.5%,而AID-DFS方案的检测率仍可达94.9%。
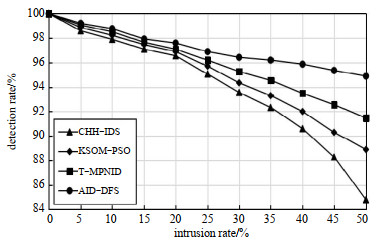 |
| Fig.4 Comparison of intrusion detection rate among four schemes 图 4 4种方案的入侵检测率比较 |
图 5给出了在不同转发调整比例ΔR下,AID-DFS入侵检测方案的TP随FP的变化而变化的情况,该性能主要用于分析AID-DFS入侵检测方案的ROC特性。由图 5可以看出,在不同的调整比例ΔR下,AID-DFS入侵检测方案的TP随FP的增加均呈现上升趋势。当ΔR=0时,AID-DFS入侵检测方案的TP最低;当ΔR=0.25时,AID-DFS入侵检测方案的TP最高。由此可知,当ΔR=0.25时,AID-DFS入侵检测方案可获得最优的ROC特性。
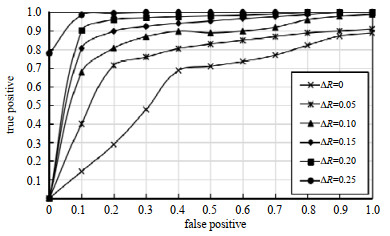 |
| Fig.5 ROC characteristics under different ΔR 图 5 不同ΔR下的ROC特性 |
精确率主要是指随查全率(Recall)变化,入侵检测方案的查准率(Precision)的变化情况。入侵检测方案的精确率越高,其性能越好,即当入侵检测方案的精确率趋于1时,表明该入侵方案的性能最好。其中,查全率的定义为:PT/(PT+NF),查准率的定义为:PT/(PT+PF)。图 6给出了不同转发调整比例ΔR下,AID-DFS的精确率曲线变化情况。由图 6可以看出,当ΔR=0时,AID-DFS入侵检测方案的精确率最低;当ΔR=0.25时,AID-DFS入侵检测方案的精确率最高。由此可知,ΔR=0.25时,AID-DFS入侵检测方案可以使系统性能达到最优,此时AID-DFS入侵检测方案的查全率为99.8%,查准率可达90.1%。
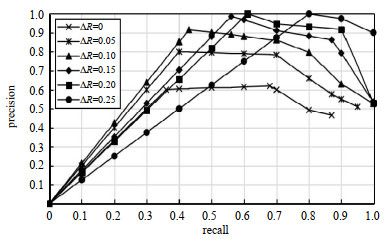 |
| Fig.6 Accuracy curves under different ΔR 图 6 不同ΔR下的精确率曲线 |
WSN当前广泛用于监测关键基础设施。为有效提升WSN入侵检测的性能,给出了一种WSN数据融合阶段的自适应入侵检测方案。方案采用基于权重的簇化WSN结构,通过跟踪异常检测子系统和误用检测子系统的接收操作特征,再根据决策函数调整转发至2个子系统的数据比例,从而有效优化WSN的入侵检测性能。仿真数据表明,所给方案的准确率和检测率分别高达99.6%和94.9%以上,比其他经典入侵检测方案分别提高了约0.5%和10.2%,且实验确定当
| [1] |
OTOUM S, KANTARCI B, MOUFTAH H T.Hierarchical trust-based black-hole detection in WSN based smart grid monitoring[C]//2017 IEEE International Conference on Communications (ICC).Paris, France: IEEE, 2017: 1-6.
|
| [2] |
苏雪, 张小云. 基于无线传感网络的高速铁路监测系统[J]. 太赫兹科学与电子信息学报, 2019, 17(2): 239-242. (SU Xue, ZHANG Xiaoyun. High-speed railway monitoring system based on wireless sensor network[J]. Journal of Terahertz Science and Electronic Information Technology, 2019, 17(2): 239-242.) |
| [3] |
陈君, 周达夫, 王飞, 等. 麦冬田间环境监测和自动灌溉系统设计与实现[J]. 太赫兹科学与电子信息学报, 2016, 14(2): 270-275. (CHEN Jun, ZHOU Dafu, WANG Fei, et al. Design and implementation of field monitoring and automatic irrigation system for radix ophiopogonis[J]. Journal of Terahertz Science and Electronic Information Technology, 2016, 14(2): 270-275.) |
| [4] |
RIZWAN R, KHAN F A, ABBAS H, et al. Anomaly detection in wireless sensor networks using immune-based bioinspired mechanism[J]. International Journal of Distributed Sensor Networks, 2015(6): 1120-1127. DOI:10.1155/2015/684952 |
| [5] |
WAZID M, DAS A K. An efficient hybrid anomaly detection scheme using K-means clustering for wireless sensor networks[J]. Wireless Personal Communications, 2016, 90(4): 1971-2000. DOI:10.1007/s11277-016-3433-3 |
| [6] |
SEDJELMACI H, SENOUCI S M, TALEB T. An accurate security game for low-resource IoT devices[J]. IEEE Transactions on Vehicular Technology, 2017, 66(10): 9381-9393. DOI:10.1109/TVT.2017.2701551 |
| [7] |
OTOUM S, KANTARCI B, MOUFTAH H T. Detection of known and unknown intrusive sensor behavior in critical applications[J]. IEEE Sensors Letters, 2017, 1(5): 1-4. DOI:10.1109/LSENS.2017.2752719 |
| [8] |
刘双, 石飞, 汪烈军, 等. 基于KSOM-PSO算法的无线传感器网络入侵检测研究[J]. 中国科技论文, 2017, 12(2): 148-153. (LIU Shuang, SHI Fei, WANG Liejun, et al. Research on intrusion detection in wireless sensor networks based on KSOM-PSO algorithm[J]. China Science Paper, 2017, 12(2): 148-153. DOI:10.3969/j.issn.2095-2783.2017.02.006) |
| [9] |
周伟伟, 郁滨. WSNs多阶段入侵检测博弈最优策略研究[J]. 电子与信息学报, 2018, 40(1): 63-71. (ZHOU Weiwei, YU Bin. Optimal defense strategy in WSNs based on the game of multi-stage intrusion detection[J]. Journal of Electronics & Information Technology, 2018, 40(1): 63-71. DOI:10.11999/JEIT170323) |
| [10] |
许力, 李光辉. 基于信任机制的无线传感器网络多协议层入侵检测方法[J]. 传感技术学报, 2019, 32(5): 739-748. (XU Li, LI Guanghui. Multi-protocol layer intrusion detection method for wireless sensor networks based on trust mechanism[J]. Chinese Journal of Sensors and Actuators, 2019, 32(5): 739-748. DOI:10.3969/j.issn.1004-1699.2019.05.018) |
| [11] |
翟继强, 马文亭, 肖亚军. Apriori-KNN算法的警报过滤机制的入侵检测系统[J]. 小型微型计算机系统, 2018, 39(12): 2632-2635. (ZHAI Jiqiang, MA Wenting, XIAO Yajun. Intrusion detection system based on Apriori-KNN algorithm for alarm filtering mechanism[J]. Journal of Chinese Systems, 2018, 39(12): 2632-2635.) |
| [12] |
曹科研, 栾方军, 孙焕良, 等. 不确定数据基于密度的局部异常点检测[J]. 计算机学报, 2017, 40(10): 2231-2244. (CAO Keyan, LUAN Fangjun, SUN Huanliang, et al. Density-based local outlier detection on uncertain data[J]. Chinese Journal of Computers, 2017, 40(10): 2231-2244. DOI:10.11897/SP.J.1016.2017.02231) |
| [13] |
熊自立, 韩兰胜, 徐行波, 等. 基于博弈的无线传感器网络入侵检测模型[J]. 计算机科学, 2017, 44(z1): 326-332. (XIONG Zili, HAN Lansheng, XU Xingbo, et al. Research on intrusion detection of wireless sensor networks based on game theory[J]. Computer Science, 2017, 44(z1): 326-332.) |
 2020, Vol. 18
2020, Vol. 18

